|
P.256の問題番号「7.3.10」
に対する解答
2次元系$\dot{\boldsymbol{x}} = A \boldsymbol{x} - r^2 \boldsymbol{x}$、$A$は固有値$\alpha \pm i \omega$をもつ。
行列$A$を
\[ A = \begin{pmatrix} \alpha & -\omega \\ \omega & \alpha \end{pmatrix} \]とおいても一般性は変わらない。
このとき、この系を極座標で表すと、
\[ \dot{r} = r ( \alpha - r^2 ), \ \ \dot{\theta} = \omega \]となる。
i) $\alpha > 0$のとき、動径方向と角度方向のダイナミクスは分離しているので、それぞれ個別にしらべる。動径方向のダイナミクスを直線上のベクトル場として取り扱うことにより、$r^*=0$は不安定固定点であり、$r^*=\sqrt{\alpha}$は安定固定点であることがわかる。したがって、相平面に戻って考えると、($r^*=0$を除く)すべての軌道は$r^*=\sqrt{\alpha}$の円に単調に近づいていくことがわかる。角度方向の運動は単に一定角速度$\omega$での回転なので、すべての軌道は$r=\sqrt{\alpha}$のリミットサイクルへ漸近的に巻き付いていく。すなわち、すくなくとも1つリミットサイクルが存在する。
ii) $\alpha < 0$のとき、$g(\boldsymbol{x})=1$と選ぶと、
\[ \nabla \cdot (g \dot{\boldsymbol{x}}) = 2(\alpha - r^2 ) < 0 \]となる。領域$R^2$は単連結であり、関数$g$および$\boldsymbol{f} = A \boldsymbol{x} - r^2 \boldsymbol{x}$は滑らかさの条件を満たしているので、デュラックの判定法により、リミットサイクルは1つも存在しない。
投稿者:goodbook
投稿日時:2021-02-13 07:12:33
|
|
|
P.256の問題番号「7.3.11」
に対する解答
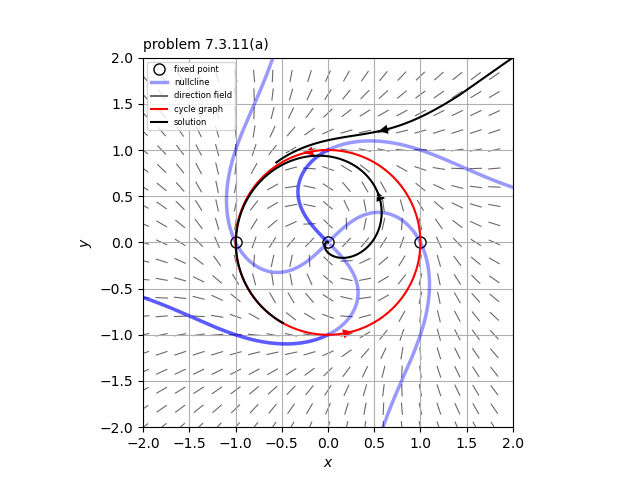
系$\dot{r} = r(1-r^2)[ r^2 \sin^2 \theta +( r^2 \cos^2 \theta -1 )^2 ]$
$dot{\theta} = r^2 \sin^2 \theta +( r^2 \cos^2 \theta -1 )^2$
(a) この系の相図は添付図のようになる。単位円上に2つの固定点$(1,0), \ \ (-1,0)$をもつ循環グラフとなる。
投稿者:goodbook
投稿日時:2021-02-13 12:26:15
|
|
|
P.256の問題番号「7.4.1」
に対する解答
方程式$\ddot{x}+\mu (x^2-1) \dot{x} + \tanh x = 0$
解)$f(x)= \mu(x^2-1), \ \ g(x)=\tanh x$とおくと、
(1) $f(x)$および$g(x)$はすべての$x$に対して連続微分可能。
(2) $g(-x) = \tanh(-x) = -\tanh x = -g(x)$となり、$g(x)$は奇関数。
(3) $x>0$に対して$g(x)=\tanh x > 0$。
(4) $f(-x)= \mu ( (-x)^2 - 1 ) = \mu (x^2-1) = f(x)$となり、$f(x)$は偶関数。
(5) $F(x)= \frac{1}{3} \mu x (x^2 - 3)$となるので、$a=\sqrt{3}$とすると、$\mu>0$のとき、$F(x)$は$x=a$でのみ$0$となり、$0<x<a$では負、$x>a$では正の値をもつ非減少関数であり、$x \to \infty$では$F(x) \to \infty$となる。
したがって、リエナールの定理より、この方程式は$\mu>0$のとき安定な周期解をちょうど1つ持つ。
投稿者:goodbook
投稿日時:2021-02-14 06:46:36
|
|
|
P.256の問題番号「7.4.2」
に対する解答
方程式$\ddot{x}+\mu (x^4-1) \dot{x} + x = 0$
(a)$f(x)= \mu(x^4-1), \ \ g(x)=x$とおくと、
(1) $f(x)$および$g(x)$はすべての$x$に対して連続微分可能。
(2) $g(-x) = -x = -g(x)$となり、$g(x)$は奇関数。
(3) $x>0$に対して$g(x)=x > 0$。
(4) $f(-x)= \mu ( (-x)^4 - 1 ) = \mu (x^4-1) = f(x)$となり、$f(x)$は偶関数。
(5) $F(x)= \frac{1}{5} \mu x (x^4 - 5)$となるので、$a=5^{\frac{1}{4}}$とすると、$\mu>0$のとき、$F(x)$は$x=a$でのみ$0$となり、$0<x<a$では負、$x>a$では正の値をもつ非減少関数であり、$x \to \infty$では$F(x) \to \infty$となる。
したがって、リエナールの定理より、この方程式は$\mu>0$で唯一の安定なリミットサイクルをもつ。
(b) 方程式をベクトル場で表すと、
$\dot{x} = y, \ \ \dot{y}=-x-\mu(x^4-1)y$
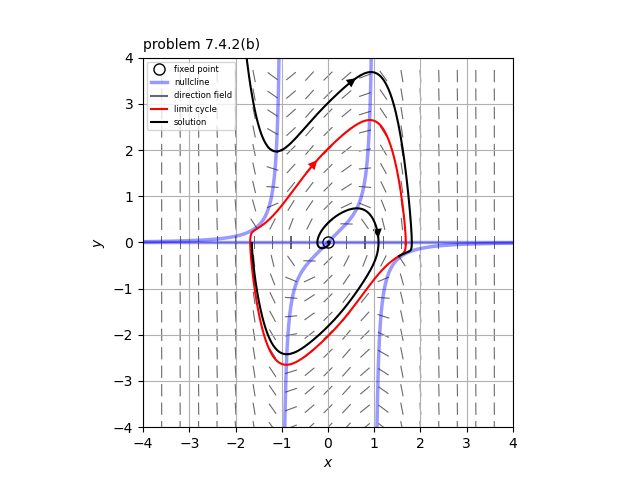
となる。この系の固定点は原点のみで、$\mu=1$のときは不安定スパイラルとなる。
$\mu=1$のときの相図は添付図のようになる。
(c) この系を時間反転した方程式は$\ddot{x}-\mu (x^4-1) \dot{x} + x = 0$となる。このとき、$f(x)= -\mu(x^4-1), \ \ g(x)=x$とおくと、$\mu<0$の場合にリエナールの定理の条件をすべて満たす(条件(5)は$a=5^{\frac{1}{4}}$で成り立つ)ので、時間反転した系は$\mu<0$で唯一の安定なリミットサイクルをもつ。したがって、$\mu<0$の場合は、唯一の不安定なリミットサイクルをもつ。
投稿者:goodbook
投稿日時:2021-02-14 08:10:10
|
|
|
P.257の問題番号「7.5.1」
に対する解答
まず$x_B$は$y=F(x)$の極小点であるので、
\[ F'(x)=x^2-1=0, \ \ F''(x)=2x>0 \]より、$x_B=1$が得られる。
次に、$x_A$は、$F(x_A)$が極大値$2/3$と同じ値をもち、かつ$x_A>0$であるので、
\[ \frac{1}{3} x^3 -x = \frac{2}{3}, \ \ \to \ \ (x+1)^2(x-2)=0 \]より、$x_A=1$が得られる。
投稿者:goodbook
投稿日時:2021-02-15 05:04:38
|
|
|
P.257の問題番号「7.5.2」
に対する解答
ファン・デル・ポール方程式$\dot{x}=y, \ \ \dot{y}=-x-\mu (x^2-1) y$
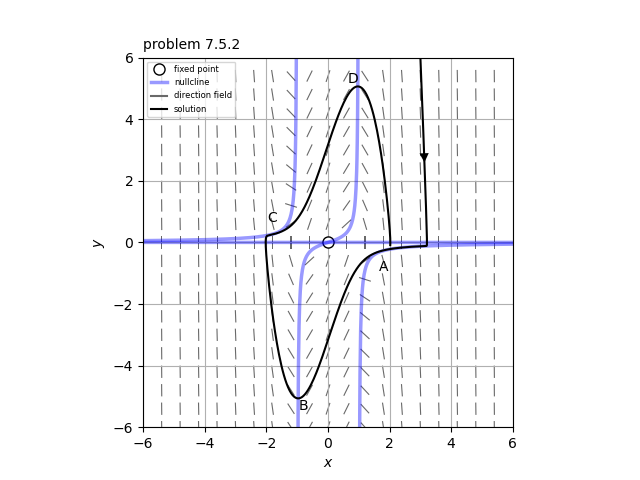
初期位置としてヌルクライン$y=\frac{x}{\mu( 1-x^2 )}$にそれほど近接していない第1象限にあり、$x^2-1 \sim \mathcal{O}(1)$となる点を考えると、$|\dot{x}| \sim \mathcal{O}(1)$で、$|\dot{y}| \sim \mathcal{O}(\mu) \gg 1$となる。したがって、ベクトル場の流れの速度は水平方向に比べて垂直方向が大きくなり、軌道はほとんど垂直方向下向き($\dot{y}<0$)に動く。やがて軌道はヌルクライン$y=\frac{x}{\mu( 1-x^2 )}, \ x>1$にきわめて近接し、$y \sim \mathcal{O}(\mu^{-1})$となる。つまり、$\dot{x} \sim \mathcal{O}(\mu^{-1})$、$\dot{y}\sim 0$となる。このとき、軌道はヌルクラインの近傍(Aのあたり)に沿ってゆっくりと移動する。その後、$|y|$の値は少しずつ大きくなり、$\dot{x} =y \sim \mathcal{O}(1)$になると、軌道はヌルクラインから離れていき、$|\dot{y}| \sim \mathcal{O}(\mu) \gg 1$で点Bのあたりまでほとんど垂直方向に素早く移動する。点Bの近傍では$x^2-1 \sim \mathcal{O}(\mu^{-1})$となるので、$|\dot{x}| \sim \mathcal{O}(1)$、$|\dot{y}| \sim \mathcal{O}(1)$で進むが、やがて$x^2-1 \sim \mathcal{O}(1)$となり、$|\dot{x}| \sim \mathcal{O}(1)$、$|\dot{y}| \sim \mathcal{O}(\mu) \gg 1$となるので、軌道はほとんど垂直方向上向き($\dot{y}>0$)に動き、やがてヌルクライン$y=\frac{x}{\mu( 1-x^2 )}, \ x<-1$にきわめて近接することになる。このとき、$\dot{x}=y \sim \mathcal{O}(\mu^{-1})$、$\dot{y} \sim 0$となり、軌道はヌルクラインの近傍(Cのあたり)に沿ってゆっくりと移動する。その後は$|y|$の値が少しずつ大きくなり、$\dot{x} \sim \mathcal{O}(1)$になると、軌道はヌルクラインから離れていき、点Dのあたりにほとんど垂直方向上向きに素早く移動し、ここを通過した後、今度は垂直方向下向き($\dot{y}<0$)に素早く動き、点A付近に戻る。以降はこの動きを繰り返す。
リエナール平面の利点としては、リミットサイクルの領域をある程度定量的に求めることができるため、リミットサイクルの周期などを見積もりやすい点などが挙げられる。
投稿者:goodbook
投稿日時:2021-02-16 06:29:47
|
|
|
P.257の問題番号「7.5.3」
に対する解答
系$\ddot{x}+k(x^2-4)\dot{x}+x=1$
解)左辺の第1項と第2項から
\[ \ddot{x}+k(x^2-4)\dot{x} = \frac{d}{dt} \left[ \dot{x} + k \left( \frac{1}{3} x^3 - 4x \right) \right] \]となるので、
\[ F(x) = \frac{1}{3} x^3 - 4x, \ \ w = \dot{x} + kF(x) \]とおくと、系は
\[ \dot{w} = \ddot{x} + k(x^2-4)\dot{x} = 1-x \]と書くことができる。したがって、系は
\[ \dot{x} = w - kF(x), \ \ \dot{w}=1-x \]となる。さらに、$w=ky$とおくと、
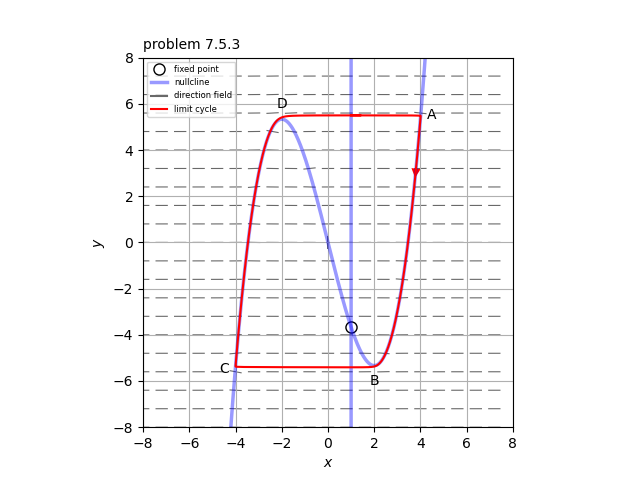
\[ \dot{x} = k( y - F(x) ), \ \ \dot{y}=\frac{1-x}{k} \]となる。このリエナール平面の相図は添付図のようになる。
次に、$k \gg 1$のとき、ヌルクライン間のジャンプに要する時間を無視できるため、周期$T$はヌルクライン上の2つの遅い枝に沿って移動するのに要する時間にほぼ相当する。したがって、
\[ T \approx 2 \int_{t_A}^{t_B}dt \]となる。遅い枝上での軌道は$y \approx F(x)$と近似できるので、
\[ \frac{dy}{dt} \approx F'(x) \frac{dx}{dt} = (x^2-4) \frac{dx}{dt} \]と$\dot{y} = (1-x)/k$より
\[ dt \approx -\frac{k(x^2-4)}{x-1} dx \]が成り立つ。また、正の方の枝は$x_A=4$から始まり、$x_B=2$で終わる。したがって、
\[ T \approx 2 \int_4^2 \frac{-k(x^2-4)}{x-1} dx = 2k [ 8-3 \ln 3 ] \]となる。
投稿者:goodbook
投稿日時:2021-02-17 05:30:58
|
|
|
P.257の問題番号「7.5.4」
に対する解答
方程式$\ddot{x}+\mu f(x) \dot{x}+x=0$
ただし、$|x|<1$で$f(x)=-1$、$|x| \geq 1$で$f(x)=1$
(a) $F(x)$を区分線形関数
\[ F(x) = \begin{cases} x+2 & (x \leq -1) \\ -x & (|x| \leq 1) \\ x-2 & (x \geq 1) \end{cases} \]とおくと、
\[ \ddot{x}+ \mu f(x) \dot{x} = \frac{d}{dt} \left[ \dot{x} + \mu F(x) \right] \]となる。$w = \dot{x} + \mu F(x)$とおくと、方程式は
\[ \dot{w} = \ddot{x} + \mu f(x) \dot{x} = -x \]と書くことができる。したがって、系は
\[ \dot{x} = w - \mu F(x), \ \ \dot{w}=-x \]となる。さらに、$w= \mu y$とおくと、系は
\[ \dot{x} = \mu ( y - F(x) ), \ \ \dot{y}=\frac{-x}{\mu} \]と等価であることがわかる。
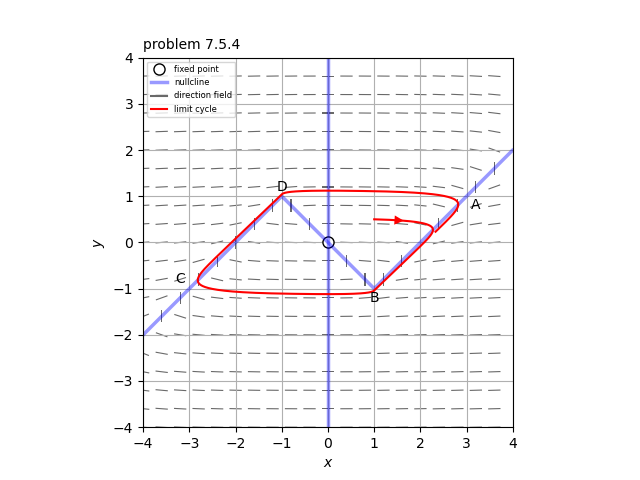
(b) ヌルクラインは添付図の青の線になる。
(c) リミットサイクルは添付図の赤線のようになる。図のB→C、D→Aのジャンプする領域では、区分線形関数で与えられるヌルクラインに近接していない$y-F(x) \sim \mathcal{O}(1)$の場合に相当し、$|\dot{x}| \sim \mathcal{O}(\mu) \gg 1, \ \ |\dot{y}| \sim \mathcal{O}(\mu^{-1}) \ll 1$となり、軌道はほとんど水平方向に$\Delta t \sim \mathcal{O}(\mu^{-1})$の短い時間で動く。一方、図のA→B、C→Dのヌルクラインに沿った領域では、$y-F(x) \sim \mathcal{O}(\mu^{-2})$と考えることができ、$|\dot{x}| \sim \mathcal{O}(\mu^{-1}) \ll 1, \ \ |\dot{y}| \sim \mathcal{O}(\mu^{-1}) \ll 1$となり、$\Delta t \sim \mathcal{O}(\mu)$の長い時間で動く。つまり、この系は$\mu \gg 1$で弛緩振動を生じる。
(d) $\mu \gg 1$の場合のリミットサイクルの周期は
\[ T \approx 2 \int_{t_A}^{t_B}dt \]となる。遅い枝上での軌道は$y \approx F(x)$と近似できるので、
\[ \frac{dy}{dt} \approx F'(x) \frac{dx}{dt} = \frac{dx}{dt} \]となる。これと$\dot{y} = -x/\mu$より
\[ dt \approx -\frac{\mu}{x} dx \]が成り立つ。また、正の方の枝は$x_A=3$から始まり、$x_B=1$で終わる。したがって、
\[ T \approx 2 \int_3^1 \frac{-\mu}{x} dx = 2 \ln 3 \mu \]となる。
投稿者:goodbook
投稿日時:2021-02-18 06:05:57
|
|
|
P.257の問題番号「7.5.5」
に対する解答
方程式$\ddot{x}+\mu (|x|-1) \dot{x}+x=0$
まず、リエナール平面を求める。$F(x)$を区分に滑らかな関数
\[ F(x) = \begin{cases} -\frac{1}{2} x^2 - x = -\frac{1}{2} (x+1)^2 + \frac{1}{2} & (x < 0) \\ \frac{1}{2} x^2 - x = \frac{1}{2} (x-1)^2 - \frac{1}{2} & (x \geq 0) \end{cases} \]とおくと、
\[ \ddot{x}+ \mu (|x|-1) \dot{x} = \frac{d}{dt} \left[ \dot{x} + \mu F(x) \right] \]となる。$w = \dot{x} + \mu F(x)$とおくと、方程式は
\[ \dot{w} = \ddot{x} + \mu (|x|-1) \dot{x} = -x \]と書くことができる。したがって、系は
\[ \dot{x} = w - \mu F(x), \ \ \dot{w}=-x \]となる。さらに、$w= \mu y$とおくと、系は
\[ \dot{x} = \mu ( y - F(x) ), \ \ \dot{y}=\frac{-x}{\mu} \]となる。
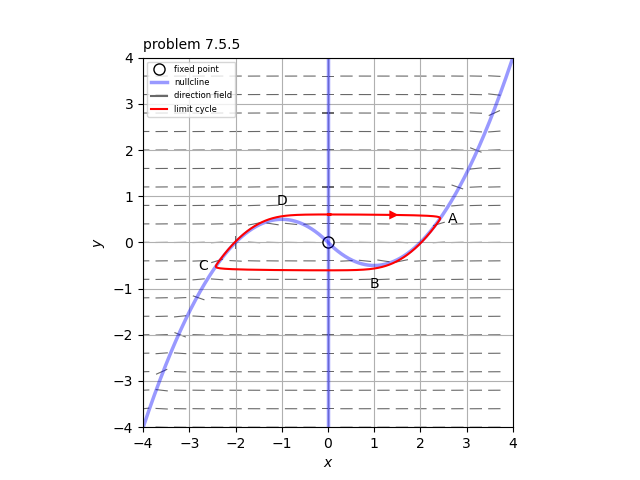
次に、$\mu \gg 1$のとき、リミットサイクルは添付図の赤線のようになり、弛緩振動を生じる。この場合のリミットサイクルの周期は
\[ T \approx 2 \int_{t_A}^{t_B}dt \]とできる。遅い枝上での軌道は$y \approx F(x)$と近似できるので、
\[ \frac{dy}{dt} \approx F'(x) \frac{dx}{dt} = (x-1)\frac{dx}{dt} \]となる。これと$\dot{y} = -x/\mu$より
\[ dt \approx -\frac{\mu(x-1)}{x} dx \]が成り立つ。また、正の方の枝は$x_A=1+\sqrt{2}$から始まり、$x_B=1$で終わる。したがって、
\[ T \approx 2 \int_{1+\sqrt{2}}^1 \frac{-\mu(x-1)}{x} dx = 2 [\sqrt{2} - \ln (\sqrt{2}+1) ] \mu \]となる。
投稿者:goodbook
投稿日時:2021-02-19 04:58:18
|
|
|
P.257の問題番号「7.5.6」
に対する解答
バイアスをかけたファン・デル・ポール振動子
$\ddot{x}+\mu (x^2-1) \dot{x}+x=a$
(a) リエナール平面で考える。$F(x)$を
\[ F(x) = \frac{1}{3} x^3 - x \]とおくと、この系は
\[ \dot{x} = \mu [ y - F(x)], \ \ \dot{y}= \frac{a-x}{\mu} \]となる。
この系の固定点は$(a,F(a))$となる。このとき、ヤコビ行列は
\[ A = \begin{pmatrix} -\mu (a^2-1) & \mu \\ -1/\mu & 0 \end{pmatrix}, \ \ \tau=-\mu(a^2-1), \ \ \Delta =1, \ \ \tau^2 -4 \Delta = \mu^2(a^2-1)^2-4 \]となる。したがって、
i) $|a|<1$のとき、$(a,F(a))$は不安定な固定点となる。
ii) $|a|=1$のとき、$(a,F(a))$はセンターと予想される。
iii) $|a|>1$のとき、$(a,F(a))$は安定な固定点となる。
(b) 2本のヌルクラインの交点が3次関数で与えられるヌルクラインの中央の枝上にあるとき、$|a|<1$となるので、(a)の結果から固定点は不安定である。
(c) $a_c=1$
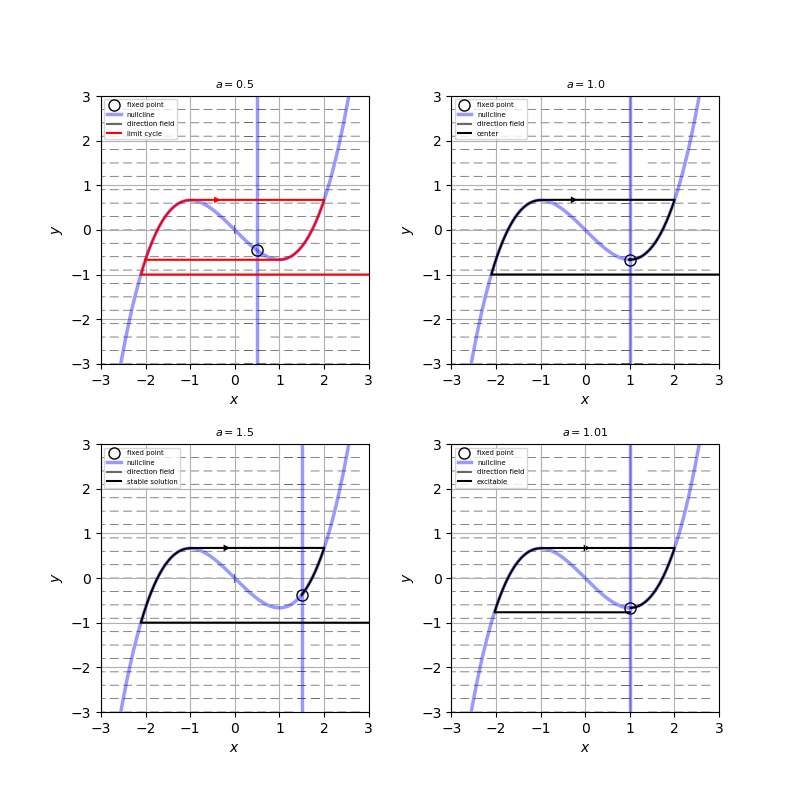
リエナール平面上で解析を行うと、$|a|<1$のときは通常のファン・デル・ポール振動子と同様の解析でリミットサイクルが存在することを示せる。一方、$|a| > 1$のとき、軌道は3次関数で与えられるヌルクラインの正または負の枝上にある安定な固定点に吸収される。$|a|=1$のとき、軌道は固定点周りの小さな周回軌道に捕らえられる。
(d) 例えば、$a=1.01$の場合の相図を添付図右下に示す。
固定点よりわずかに下の位置から始まる軌道は一旦、3次関数で与えられるヌルクラインの負の枝まで水平方向に移動し、負の枝に沿って上った後、正の枝に水平方向にジャンプする。そして、正の枝上に沿ってゆっくり下りていき、安定な固定点に吸収される。すなわち、興奮性であることがわかる。
投稿者:goodbook
投稿日時:2021-02-20 14:22:11
|
|





