|
P.254の問題番号「7.2.11」
に対する解答
\[ V = ax^2 +2bxy +cy^2 = a \left( x + \frac{b}{a}y \right)^2 + \frac{ac-b^2}{a} y^2 \]と変形できるので、$V$が正定値となるためには$a>0$かつ$ac-b^2>0$であることと同値であることがわかる。
投稿者:goodbook
投稿日時:2021-01-23 17:31:33
|
|
|
P.255の問題番号「7.3.1」
に対する解答
7.3.1
系$\dot{x}=x-y-x(x^2+5y^2), \ \ \dot{y} = x+y-y(x^2+y^2)$
(a) 原点でのヤコビ行列は
\[ A = \begin{pmatrix} 1-3x^2-5y^2 & -1-10xy \\ 1-2xy & 1-x^2-3y^2 \end{pmatrix}=\begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}, \ \ \tau=2, \ \ \Delta =2, \ \ \tau^2 -4 \Delta = -4 \]となるので、不安定スパイラルとなる。
(b) $ \dot{r} = r - r^3 (1+\sin^2 2 \theta), \ \ \dot{\theta} = 1 + r^2 \sin 2\theta ( 1- \cos 2\theta )$
(c) 原点を中心とする円で、その上ですべての軌道が動径方向に外向きの成分をもつためには、$\dot{r}>0$が任意の$\theta$について成り立てばよい。つまり、
\[ r^2 < \frac{1}{1+\sin^2 2 \theta} \]が任意の$\theta$で成り立つ。$1 \leq 1+\sin^2 2 \theta \leq 2$であるので、外向きの成分をもつような最大半径は
\[ r_1 = \frac{1}{\sqrt{2}} \]となる。
(d) 原点を中心とする円で、その上ですべての軌道が動径方向に内向きの成分をもつためには、$\dot{r}<0$が任意の$\theta$について成り立てばよい。つまり、
\[ r^2 > \frac{1}{1+\sin^2 2 \theta} \]が任意の$\theta$で成り立つ。$1 \leq 1+\sin^2 2 \theta \leq 2$であるので、内向きの成分をもつような最大半径は
\[ r_2 = 1 \]となる。
(e) この系とトラッピング領域$r_1 \leq r \leq r_2$はポアンカレ-ベンディクソンの定理の仮定を満たすので、このトラッピング領域にリミットサイクルを持つ。
投稿者:goodbook
投稿日時:2021-01-30 14:34:42
|
|
|
P.255の問題番号「7.3.2」
に対する解答
演習問題7.3.1の系$\dot{x}=x-y-x(x^2+5y^2), \ \ \dot{y} = x+y-y(x^2+y^2)$の相図は添付図のようになる。
添付図よりリミットサイクルがトラッピング領域内にあることがわかる。

投稿者:goodbook
投稿日時:2021-01-31 08:46:59
|
|
|
P.255の問題番号「7.3.3」
に対する解答
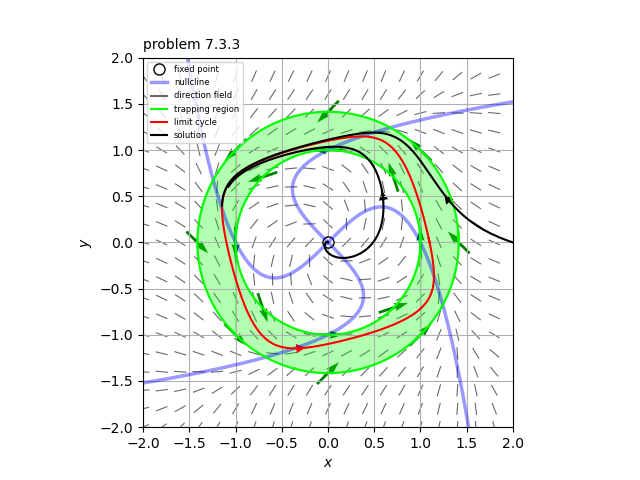
系$\dot{x}=x-y-x^3, \ \ \dot{y} = x+y-y^3$
この系は原点に固定点を持つ。原点でのヤコビ行列は
\[ A = \begin{pmatrix} 1-3x^2 & -1 \\ 1 & 1-3y^2 \end{pmatrix}=\begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}, \ \ \tau=2, \ \ \Delta =2, \ \ \tau^2 -4 \Delta = -4 \]となるので、不安定スパイラルとなる。
次に、この系を極座標で表すと、
\[ \dot{r} = r - \frac{r^3}{4} (3+\cos 4 \theta), \ \ \dot{\theta} = 1 - \frac{r^2}{4} \sin 4 \theta \]となる。
原点を中心とする円で、その上ですべての軌道が動径方向に外向きの成分をもつためには、任意の$\theta$について$\dot{r}>0$、すなわち、
\[ r^2 < \frac{4}{3+\cos 4 \theta} \]となる$r$を選べばよい。$1 \leq 4/(3+\cos 4 \theta ) \leq 2$であるので、これを満たす最大半径は
\[ r_1 = 1 \]となる。一方、原点を中心とする円で、その上ですべての軌道が動径方向に内向きの成分をもつためには、任意の$\theta$について$\dot{r}<0$、すなわち、
\[ r^2 > \frac{4}{3+\cos 4 \theta} \]となる$r$を選べばよい。$1 \leq 4/(3+\cos 4 \theta ) \leq 2$であるので、これを満たす最小半径は
\[ r_2 = \sqrt{2} \]となる。
したがって、この系とトラッピング領域$r_1 \leq r \leq r_2$はポアンカレ-ベンディクソンの定理の仮定を満たすので、このトラッピング領域に周期解を持つ。
投稿者:goodbook
投稿日時:2021-02-01 05:11:49
|
|
|
P.255の問題番号「7.3.4」
に対する解答
系$\dot{x} = x(1-4x^2-y^2) - \frac{1}{2}y(1+x), \ \ \dot{y} = y(1-4x^2-y^2) + 2x(1+x)$
(a) この系の固定点は原点のみ。原点でのヤコビ行列は
\[ A = \begin{pmatrix} 1-12x^2 - y^2 -\frac{1}{2} y & -2xy - \frac{1}{2}(1+x) \\ -8xy+2+4x & 1-4x^2-3y^2 \end{pmatrix}=\begin{pmatrix} 1 & -\frac{1}{2} \\ 2 & 1 \end{pmatrix}, \\ \tau=2, \ \ \Delta =2, \ \ \tau^2 -4 \Delta = -4 \]となるので、不安定スパイラルとなる。
(b) $V=(1-4x^2-y^2)^2$として、$\dot{V}$を考えると、
\[ \dot{V} = -4(1-4x^2-y^2)(4x\dot{x}+y\dot{y}) = -4(4x^2+y^2)(1-4x^2-y^2)^2 \leq 0 \]となる。これは原点を除く任意の点から始まる軌道は時間が経つにつれて、$V$が小さくなる向きに進み、やがて楕円$4x^2+y^2=1$に近づいていくと、$\dot{V}$は$0$に近づき、この楕円近傍に留まり続けることを表している。つまり、すべての軌道が$t \to \infty$で楕円$4x^2+y^2=1$に近づいていくことが分かる。
投稿者:goodbook
投稿日時:2021-02-02 05:16:02
|
|
|
P.255の問題番号「7.3.5」
に対する解答
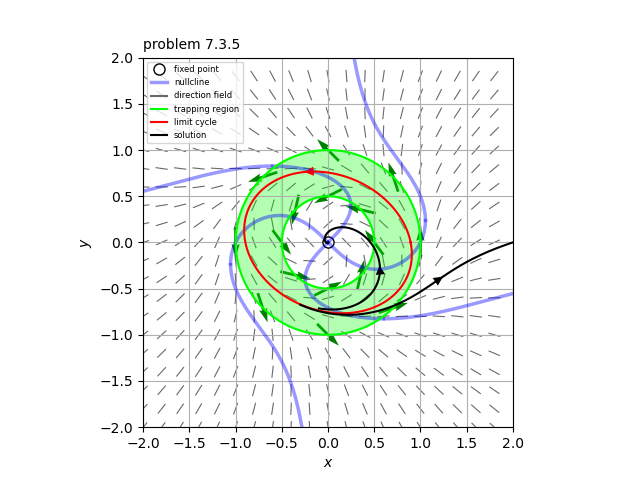
系$\dot{x}=-x-y+x(x^2+2y^2), \ \ \dot{y} = x-y+y(x^2 + 2 y^2)$
この系は原点に固定点を持つ。原点でのヤコビ行列は
\[ A = \begin{pmatrix} -1+3x^2+2y^2 & -1 +4xy\\ 1+2xy & -1 + x^2+6y^2 \end{pmatrix}=\begin{pmatrix} -1 & -1 \\ 1 & -1 \end{pmatrix}, \ \ \tau=-2, \ \ \Delta =2, \ \ \tau^2 -4 \Delta = -4 \]となるので、安定スパイラルとなる。
ここで、この系を時間反転($t \to -t$)した系
$\dot{x}=x+y-x(x^2+2y^2), \ \ \dot{y} = -x+y-y(x^2 + 2 y^2)$
を考える。この場合、原点は不安定スパイラルとなる。
次に、時間反転した系を極座標で表すと、
\[ \dot{r} = r - \frac{r^3}{2} (3+\cos 2 \theta), \ \ \dot{\theta} = -1 \]となる。
原点を中心とする円で、その上ですべての軌道が動径方向に外向きの成分をもつためには、任意の$\theta$について$\dot{r}>0$、すなわち、
\[ r^2 < \frac{2}{3+\cos 2 \theta} \]となる$r$を選べばよい。$1/2 \leq 2/(3+\cos 2 \theta ) \leq 1$であるので、これを満たす最大半径は
\[ r_1 = \frac{1}{\sqrt{2}} \]となる。一方、原点を中心とする円で、その上ですべての軌道が動径方向に内向きの成分をもつためには、任意の$\theta$について$\dot{r}<0$、すなわち、
\[ r^2 > \frac{2}{3+\cos 2 \theta} \]となる$r$を選べばよい。$1/2 \leq 2/(3+\cos 2 \theta ) \leq 1$であるので、これを満たす最小半径は
\[ r_2 = 1 \]となる。
したがって、時間反転した系とトラッピング領域$r_1 \leq r \leq r_2$はポアンカレ-ベンディクソンの定理の仮定を満たすので、このトラッピング領域に周期解を持つことがわかる。最後に周期解は時間反転しても周期解となるので、元の系にも少なくとも1つは周期解を持つことがわかる。
投稿者:goodbook
投稿日時:2021-02-03 05:37:17
|
|
|
P.255の問題番号「7.3.6」
に対する解答
振り子の方程式$\ddot{x}+F(x,\dot{x})\dot{x}+x = 0$
ただし、$r^2 = x^2 + \dot{x}^2$として、$r \leq a$で$F(x,\dot{x})<0$、$r \geq b$で$F(x,\dot{x})>0$。
(a) $F(x,\dot{x})\dot{x}$の項は振り子の減衰項とみなすことができる。
$r \leq a$のとき$F(x,\dot{x})<0$となるので、減衰項は振り子の振幅が増幅される方向に働き、一方、$r \geq b$のとき$F(x,\dot{x})>0$となるので、減衰項は振り子の振幅が減衰される方向に働く。
(b)$\dot{x}=y$とおくと、方程式は
$\dot{x}=y, \ \ \dot{y}=-x - F(x,y) y$
と表すことができる。
この系は原点に唯一の固定点をもつ。ヤコビ行列は
\[ A = \begin{pmatrix} 0 & 1 \\ -1-\frac{\partial F}{\partial x}y & -\frac{\partial F}{\partial y}y -F \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ -1 & -F(0,0) \end{pmatrix}, \ \ \tau=-F(0,0)>0, \ \ \Delta =1 \]となるので、不安定な固定点となる。
次に、この系を極座標で表すと、
\[ \dot{r} = - rF \frac{1-\cos 2 \theta }{2}, \ \ \dot{\theta} = - \left( \frac{F}{2} \sin 2 \theta + 1 \right) \]となる。$0 \leq (1-\cos 2 \theta )/2 \leq 1$であるので、$F(x,y)$の仮定から、$a \leq r \leq b$の領域はトラッピング領域とみなすことができる。したがって、ポアンカレ-ベンディクソンの定理より、$a<r<b$の領域に少なくとも1つ閉軌道が存在することがわかる。
投稿者:goodbook
投稿日時:2021-02-04 06:23:40
|
|
|
P.255の問題番号「7.3.7」
に対する解答
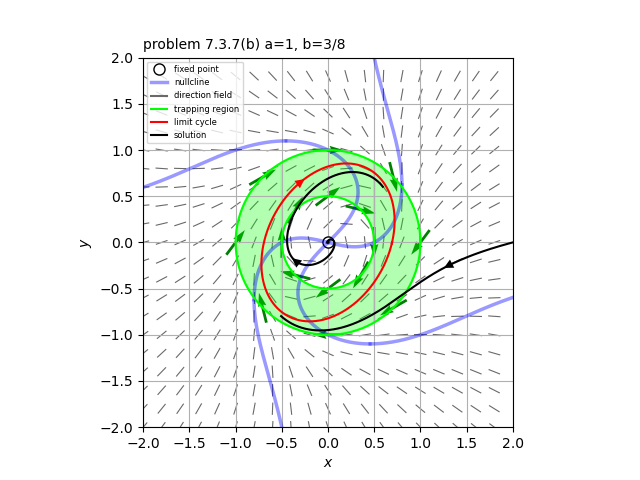
系$\dot{x}=y + ax(1-2b-r^2), \ \ \dot{y} = -x + a y (1-r^2), \ \ 0 < a \leq 1, \ \ 0 \leq b < \frac{1}{2}$
(a) この系を極座標で表すと、
\[ \dot{r} = a r ( 1 - b ( \cos 2 \theta + 1 ) - r^2 ), \ \ \ \dot{\theta} = -1 +ab \sin 2 \theta \]となる。
(b) この系は原点に固定点を持つ。原点でのヤコビ行列は
\[ A =\begin{pmatrix} a(1-2b) & 1 \\ -1 & a \end{pmatrix}, \\ \tau=2a(1-b)>0, \ \ \Delta = a^2 (1-2b) + 1 >0, \ \ \tau^2 -4 \Delta = 4(a^2 b^2-1) <0 \]となるので、不安定スパイラルとなる。
次に、原点を中心とする円で、その上ですべての軌道が動径方向に外向きの成分をもつためには、任意の$\theta$について$\dot{r}>0$、すなわち、
\[ r^2 < 1 - b( \cos 2 \theta + 1 ) \]となる$r$を選べばよい。$1-2b \leq 1 - b( \cos 2 \theta + 1 ) \leq 1$であるので、これを満たす最大半径は
\[ r_1 = \sqrt{1-2b} \]となる。一方、原点を中心とする円で、その上ですべての軌道が動径方向に内向きの成分をもつためには、任意の$\theta$について$\dot{r}<0$、すなわち、
\[ r^2 > 1 - b( \cos 2 \theta + 1 ) \]となる$r$を選べばよい。$1-2b \leq 1 - b( \cos 2 \theta + 1 ) \leq 1$であるので、これを満たす最小半径は
\[ r_2 = 1 \]となる。
したがって、この系とトラッピング領域$r_1 \leq r \leq r_2$はポアンカレ-ベンディクソンの定理の仮定を満たすので、少なくとも1つはリミットサイクルが存在する。
また、リミットサイクルの周期は
\[ T(a,b) = \int_0^{2 \pi} \frac{dt}{d \theta} d \theta = \int_0^{2 \pi} \frac{d \theta}{1 -a b \sin 2 \theta } = \int_0^{2 \pi} \frac{d \theta}{1 -a b \sin \theta } = \frac{2 \pi}{ \sqrt{1-a^2 b^2} } \]となる。
投稿者:goodbook
投稿日時:2021-02-06 09:57:56
|
|
|
P.255の問題番号「7.3.8」
に対する解答
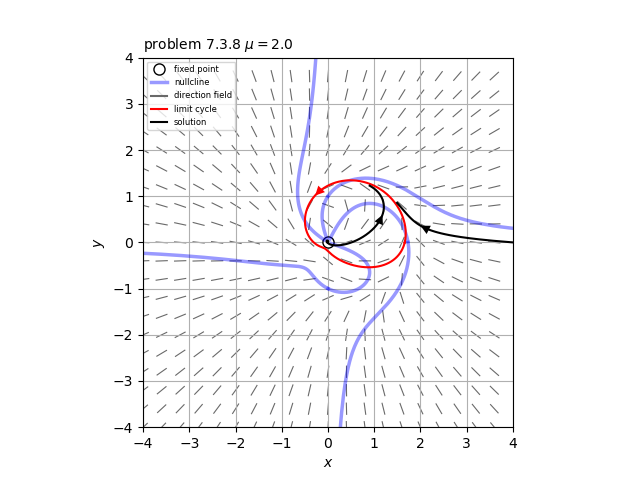
系$\dot{r}=r(1-r^2) + \mu r \cos \theta, \ \ \dot{\theta} = 1$
$\mu<1$の場合は、例題7.3.1でポアンカレ-ベンディクソンの定理により閉軌道が存在することが示されているので、$\mu \geq 1$について、さまざまな値に対して相図をプロットしてみた。その結果、$\mu$が大きくなるにつれて、閉軌道は下部の方が原点に近づいていくことがわかる。閉軌道が存在しなくなる臨界があるとすれば、この閉軌道が原点を通るときであると考えられる。そこで、原点近傍での軌道のふるまいを考えてみると、系は
$\dot{r} \approx r + \mu r \cos \theta, \ \ \dot{\theta} = 1$
に従うと考えられる。このとき、任意の$\theta$に対して、
$ 1+ \mu \cos \theta \geq 1-\mu$
であるので、ある原点近傍の点$( r_0, \theta_0 )$から出発する軌道は、時間$t$が経過しても動径方向が$r_0 e^{(1-\mu)t} >0$より小さくなることはない。したがって、閉軌道は原点を通ることはないので、閉軌道はすべての$\mu>0$に対して存在する。
投稿者:goodbook
投稿日時:2021-02-11 08:17:44
|
|
|
P.256の問題番号「7.3.9」
に対する解答
系$\dot{r}=r(1-r^2) + \mu r \cos \theta, \ \ \dot{\theta} = 1$
(a) $r(\theta) = 1+ \mu r_1( \theta ) + \mathcal{O} ( \mu^2 ) $とおく。このとき、
\[ \frac{d r}{d \theta} = \frac{ \dot{r} }{ \dot{\theta} } = r(1-r^2) + \mu r \cos \theta \]となるので、この式に$r(\theta)$を代入すると、$r_1(\theta)$の式として、\[ \frac{d r_1}{d \theta} = -2 r_1 + \cos \theta \]となる。この方程式を解いて、$r_1(\theta)$を陽に求めると、
\[ r_1(\theta) = \frac{1}{5} ( \sin \theta + 2 \cos \theta ) + C e^{-2 \theta} = \frac{1}{\sqrt{5}} \sin ( \theta + \alpha ) + C e^{-2 \theta} \]となる。ここで、$\sin \alpha = 2/\sqrt{5}, \ \ \cos \alpha = 1/\sqrt{5}$であり、$C$は積分定数である。
(b) $\theta$がある程度大きくなると、定数項$Ce^{-2 \theta}$は無視できる。このとき、$-1/\sqrt{5} \leq r_1 \leq 1/\sqrt{5}$となるので、
\[ 1-\frac{\mu}{\sqrt{5}} \leq r \leq 1+\frac{\mu}{\sqrt{5}} \]となる。一方、$\mu \ll 1$のとき、
\[ \sqrt{1 \pm \mu} \approx 1 \pm \frac{1}{2} \mu \]であるので、求めた近似解は$\sqrt{1-\mu} < r < \sqrt{1+\mu}$の円環内に存在することがわかる。
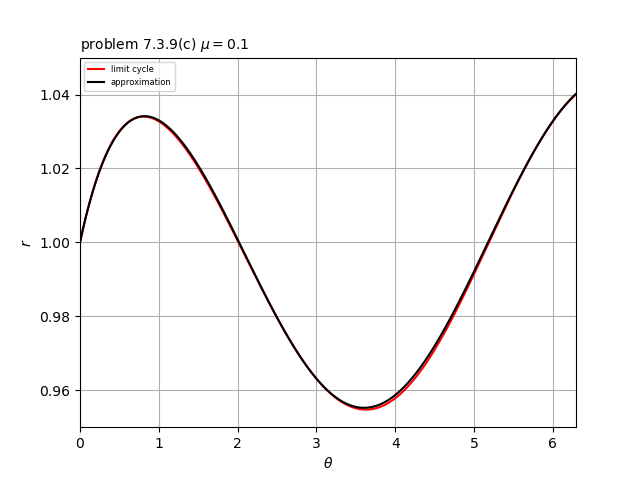
(c) $\mu=0.1$のときの数値解と近似解のプロットを添付図に示す。
その他にもいくつかの$\mu$でプロットした結果、両者の最大誤差は$\mu^2/10$程度であることが分かった。
投稿者:goodbook
投稿日時:2021-02-11 13:35:58
|
|





