|
P.258の問題番号「7.5.7」
に対する解答
系$\dot{u} = b (v-u)(\alpha + u^2 )-u, \ \ \dot{v} = c-u$
ただし、$b \gg 1, \ \ \alpha \ll 1, \ \ 8 \alpha b < 1$。
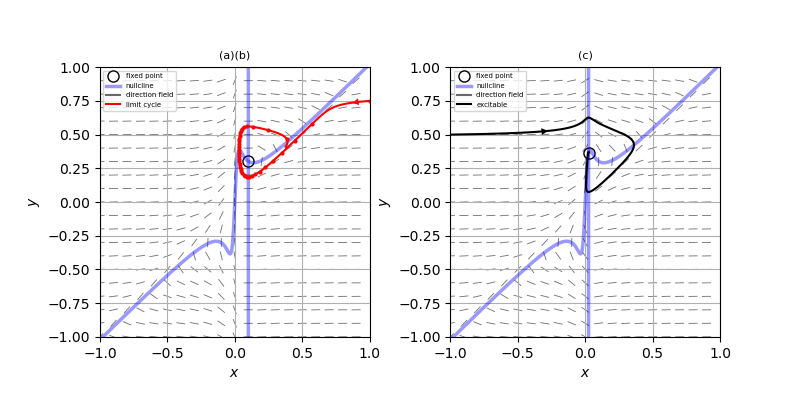
(a) $\alpha = 0.001, \ \ 8 \alpha b =0.36$としたときのヌルクラインは添付図の青線のようになる。
(b) この系の固定点は
\[ \left( c, c+ \frac{c}{b(\alpha + c^2 )} \right) \]である。このとき、ヤコビ行列は
\[ A = \begin{pmatrix} \frac{2c^2}{\alpha + c^2} -bc^2 -b \alpha -1 & b(\alpha + c^2) \\ -1 & 0 \end{pmatrix}, \\ \tau=\frac{2c^2}{\alpha + c^2} -bc^2 -b \alpha -1, \ \ \Delta =b(\alpha + c^2) \]となる。したがって、この系が弛緩振動をもつためには、少なくとも固定点が不安定である必要があるので、$\tau > 0$より、
\[ \sqrt{ \frac{ 1-2\alpha b - \sqrt{1-8 \alpha b} }{2b} } < c < \sqrt{ \frac{ 1-2\alpha b + \sqrt{1-8 \alpha b} }{2b} } \]が得られる。次に、
\[ c = \sqrt{ \frac{ 1-2\alpha b }{2b} } \]とおいたときの軌道を描くと、添付図左図の赤線のようになり、リミットサイクルが現れることがわかる。また、赤の点列は等時間間隔での軌道のプロットを表しており、$y$軸近傍では軌道はゆっくりと動き、$y$軸から離れると素早く動いていることがわかる。つまり、この系は弛緩振動をしている。以上から、\[ c_1 = \sqrt{ \frac{ 1-2\alpha b - \sqrt{1-8 \alpha b} }{2b} }, \ \ c_2 = \sqrt{ \frac{ 1-2\alpha b + \sqrt{1-8 \alpha b} }{2b} } \]と近似的に置くことができる。
(c) 添付図右図のように、$c$が$c_1$より少し小さい場合、系は興奮性となることがわかる。
投稿者:goodbook
投稿日時:2021-02-21 12:31:23
|
|
|
P.258の問題番号「7.6.1」
に対する解答
\[ x(t, \varepsilon) = (1-\varepsilon^2)^{-\frac{1}{2}} e^{-\varepsilon t} \sin \left[ (1-\varepsilon^2)^{\frac{1}{2}} t \right] \]
右辺の各項は、
\[ \begin{align}
( 1-\varepsilon^2 )^{-\frac{1}{2}} &= 1 + \mathcal{O}(\varepsilon^2) \\
e^{-\varepsilon t} &= 1 - \varepsilon t + \mathcal{O}(\varepsilon^2) \\
\sin \left[ (1 - \varepsilon^2)^{-\frac{1}{2}} \right] &= \sin t + \mathcal{O}(\varepsilon^2)
\end{align}
\]となるので、
\[ x(t,\varepsilon) = \sin t - \varepsilon t \sin t + \mathcal{O}(\varepsilon^2) \]が得られる。
投稿者:goodbook
投稿日時:2021-02-24 04:42:02
|
|
|
P.258の問題番号「7.6.2」
に対する解答
初期値問題$\ddot{x}+x+ \varepsilon x = 0, \ \ x(0)=1, \ \ \dot{x}(0) = 0 $
(a) 初期条件$x(0)=1, \ \ \dot{x}(0) = 0 $の下での$\ddot{x} + (1+\varepsilon) x = 0$の厳密解は$x(t) = \cos t$となる。
(b) 級数展開$x(t,\varepsilon) = x_0(t) + \varepsilon x_1(t) + \varepsilon^2 x_2(t) + \mathcal{O}(\varepsilon^3)$を代入すると、
\[ (\ddot{x}_0 + x_0) + \varepsilon ( \ddot{x}_1 + x_1 + x_0 ) + \varepsilon^2 ( \ddot{x}_2 + x_2 + x_1 )+ \mathcal{O}(\varepsilon^3) = 0 \]となる。この式はすべての十分小さい$\varepsilon$に対して成立するので、$\varepsilon$のそれぞれのべきの項の係数はいずれも$0$になる。したがって、
\[ \begin{align}
\mathcal{O}(1) &: \ddot{x}_0 + x_0 = 0 \\
\mathcal{O}(\varepsilon) &: \ddot{x}_1 + x_1 + x_0 = 0 \\
\mathcal{O}(\varepsilon^2) &: \ddot{x}_2 + x_2 + x_1 = 0
\end{align}
\]となる。同様の理由から、初期条件についても
\[ x_0(0) = 1, \ \ x_1(0) = 0, \ \ x_2(0) = 0, \\
\dot{x}_0(0) = 0, \ \ \dot{x}_1(0) = 0, \ \ \dot{x}_2(0) = 0 \]となる。以下、各オーダーで初期値問題を1つずつ解いていく。
$x_0(0) = 1, \ \ \dot{x}_0(0) = 0$のもとで、$\ddot{x}_0 + x_0 = 0$を解くと、
\[ x_0(t) = \cos t \]が得られる。次に、$x_1(0) = 0, \ \ \dot{x}_1(0) = 0$のもとで、$\ddot{x}_1 + x_1 + x_0 = 0$を解くと、
\[ x_1(t) = -\frac{1}{2} t \sin t \]が得られる。さらに、$x_2(0) = 0, \ \ \dot{x}_2(0) = 0$のもとで、$\ddot{x}_2 + x_2 + x_1 = 0$を解くと、
\[ x_2(t) = \frac{1}{8} t \sin t - \frac{1}{8} t^2 \cos t \]が得られる。
投稿者:goodbook
投稿日時:2021-02-25 06:07:00
|
|
|
P.258の問題番号「7.6.3」
に対する解答
初期値問題$\ddot{x}+x = \varepsilon, \ \ x(0)=1, \ \ \dot{x}(0) = 0 $
(a) 初期条件$x(0)=1, \ \ \dot{x}(0) = 0 $の下での$\ddot{x} + x - \varepsilon = 0$の厳密解は$x(t) = \cos t + \varepsilon ( 1 - \cos t )$となる。
(b) 級数展開$x(t,\varepsilon) = x_0(t) + \varepsilon x_1(t) + \varepsilon^2 x_2(t) + \mathcal{O}(\varepsilon^3)$を代入すると、
\[ (\ddot{x}_0 + x_0) + \varepsilon ( \ddot{x}_1 + x_1 - 1 ) + \varepsilon^2 ( \ddot{x}_2 + x_2 )+ \mathcal{O}(\varepsilon^3) = 0 \]となる。この式はすべての十分小さい$\varepsilon$に対して成立するので、$\varepsilon$のそれぞれのべきの項の係数はいずれも$0$になる。したがって、
\[ \begin{align}
\mathcal{O}(1) &: \ddot{x}_0 + x_0 = 0 \\
\mathcal{O}(\varepsilon) &: \ddot{x}_1 + x_1 - 1 = 0 \\
\mathcal{O}(\varepsilon^2) &: \ddot{x}_2 + x_2 = 0
\end{align}
\]となる。同様の理由から、初期条件についても
\[ x_0(0) = 1, \ \ x_1(0) = 0, \ \ x_2(0) = 0, \\
\dot{x}_0(0) = 0, \ \ \dot{x}_1(0) = 0, \ \ \dot{x}_2(0) = 0 \]となる。以下、各オーダーで初期値問題を1つずつ解いていく。
$x_0(0) = 1, \ \ \dot{x}_0(0) = 0$のもとで、$\ddot{x}_0 + x_0 = 0$を解くと、
\[ x_0(t) = \cos t \]が得られる。次に、$x_1(0) = 0, \ \ \dot{x}_1(0) = 0$のもとで、$\ddot{x}_1 + x_1 - 1 = 0$を解くと、
\[ x_1(t) = 1 - \cos t \]が得られる。さらに、$x_2(0) = 0, \ \ \dot{x}_2(0) = 0$のもとで、$\ddot{x}_2 + x_2 = 0$を解くと、
\[ x_2(t) = 0 \]が得られる。
(c) (b)の結果から摂動解は永年項を含んでいない。このようになる理由は、厳密解が正弦波振動に相当するタイムスケール$t \sim \mathcal{O}(\varepsilon^0)$のみ含んでおり、遅いタイムスケール$t \sim \mathcal{O}(\varepsilon^{-1})$を含んでいないからである。
投稿者:goodbook
投稿日時:2021-02-26 04:31:20
|
|
|
P.258の問題番号「7.6.4」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = x$
解)この系では$h=r \cos \theta$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = r \langle \sin \theta \cos \theta \rangle = 0, \\
r \phi' = \langle h \cos \theta \rangle = r \langle \cos^2 \theta \rangle = \frac{1}{2} r \]となる。よって、$A, \ \ \phi_0$をある定数として
\[ r(T) \equiv A, \ \ \phi(T) = \frac{T}{2} + \phi_0 \]となるので、長時間挙動として、単純な調和振動子の中にゆっくりと変動する位相を持つことがわかる。また、振幅はほぼ一定値をとり、振動数は$1+\varepsilon/2$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$のとき、
\[ x(t, \varepsilon) \approx a \cos \left( t + \frac{\varepsilon t}{2} \right) + \mathcal{O}( \varepsilon ) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 12:56:14
|
|
|
P.259の問題番号「7.6.5」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = x \dot{x}^2$
解)この系では$h=r^3 \sin^2 \theta \cos \theta$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = r^3 \langle \sin^3 \theta \cos \theta \rangle = 0, \\
r \phi' = \langle h \cos \theta \rangle = r^3 \langle \sin^2 \theta \cos^2 \theta \rangle = \frac{1}{8} r^3 \]となる。よって、$A, \ \ \phi_0$をある定数として
\[ r(T) \equiv A, \ \ \phi(T) = \frac{A^2}{8}T + \phi_0 \]となるので、長時間挙動として、単純な調和振動子の中にゆっくりと変動する位相を持つことがわかる。また、振幅はほぼ一定値$A$をとり、振動数は$1+\frac{A^2}{8}\varepsilon$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$のとき、
\[ x(t, \varepsilon) \approx a \cos \left( t + \frac{\varepsilon a^2 t}{8} \right) + \mathcal{O}( \varepsilon ) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 13:09:14
|
|
|
P.259の問題番号「7.6.6」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = x \dot{x}$
解)この系では$h=-r^2 \sin \theta \cos \theta$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = -r^2 \langle \sin^2 \theta \cos \theta \rangle = 0, \\
r \phi' = \langle h \cos \theta \rangle = -r^2 \langle \sin \theta \cos^2 \theta \rangle = 0 \]となる。よって、$A, \ \ \phi_0$をある定数として
\[ r(T) \equiv A, \ \ \phi(T) \equiv \phi_0 \]となるので、長時間挙動として、単純な調和振動子と同等になる。また、振幅はほぼ一定値をとり、振動数は$1+\mathcal{O}(\varepsilon^2)$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$のとき、
\[ x(t, \varepsilon) \approx a \cos t + \mathcal{O}( \varepsilon ) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 13:18:40
|
|
|
P.259の問題番号「7.6.7」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = (x^4-1) \dot{x}$
解)この系では$h=-r \sin \theta ( r^4 \cos^4 \theta - 1 )$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = -r^5 \langle \sin^2 \theta \cos^4 \theta \rangle + r \langle \sin^2 \theta \rangle = \frac{1}{2}r - \frac{1}{16} r^5, \\
r \phi' = \langle h \cos \theta \rangle = -r^5 \langle \sin \theta \cos^5 \theta \rangle + r \langle \sin \theta \cos \theta \rangle = 0 \]となる。
\[ r' = \frac{1}{16} r (8-r^4) \]は$r \geq 0$の半直線上のベクトル場に対応すると見なせるので、$r^* = 0$は不安定固定点、$r^*= \sqrt{2 \sqrt{2}}$は安定固定点となる。一方、$\phi' = 0$より、ある定数$\phi_0$に対して$\phi(T) \equiv \phi_0$となる。したがって、長時間挙動は
\[ x(t) \to \sqrt{2 \sqrt{2}} \cos ( t+ \phi_0 ) + \mathcal{O}(\varepsilon) \]となり、$x(t)$は半径$\sqrt{2 \sqrt{2}} + \mathcal{O}(\varepsilon)$の安定なリミットサイクルに近づいていく。つまり、振幅は$\sqrt{2 \sqrt{2}} + \mathcal{O}(\varepsilon)$、振動数は$1 + \mathcal{O}(\varepsilon^2)$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$として、平均化方程式を解くと、
\[ r(T) \approx \left( \frac{8 a^4}{a^4 - (a^4 - 8) e^{-2 T} } \right)^{\frac{1}{4}} + \mathcal{O}(\varepsilon), \ \ \phi_0 = \mathcal{O}(\varepsilon) \]となるので、
\[ x(t, \varepsilon) \approx \left( \frac{8 a^4}{a^4 - (a^4 - 8) e^{-2 \varepsilon t} }\right)^{\frac{1}{4}} \cos t + \mathcal{O}( \varepsilon ) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 14:44:48
|
|
|
P.259の問題番号「7.6.8」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = (|x|-1) \dot{x}$
解)この系では$h=-r \sin \theta ( r | \cos \theta | - 1 )$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = -r^2 \langle \sin^2 \theta |\cos \theta| \rangle + r \langle \sin^2 \theta \rangle = \frac{1}{2}r - \frac{2}{3 \pi} r^2, \\
r \phi' = \langle h \cos \theta \rangle = -r^2 \langle \sin \theta \cos \theta | \cos \theta | \rangle + r \langle \sin \theta \cos \theta \rangle = 0 \]となる。
\[ r' = \frac{2}{3 \pi} r (\frac{3 \pi}{4}-r) \]は$r \geq 0$の半直線上のベクトル場に対応すると見なせるので、$r^* = 0$は不安定固定点、$r^*= \frac{3 \pi}{4}$は安定固定点となる。一方、$\phi' = 0$より、ある定数$\phi_0$に対して$\phi(T) \equiv \phi_0$となる。したがって、長時間挙動は
\[ x(t) \to \frac{3 \pi}{4} \cos ( t+ \phi_0 ) + \mathcal{O}(\varepsilon) \]となり、$x(t)$は半径$\frac{3 \pi}{4} + \mathcal{O}(\varepsilon)$の安定なリミットサイクルに近づいていく。つまり、振幅は$\frac{3 \pi}{4} + \mathcal{O}(\varepsilon)$、振動数は$1 + \mathcal{O}(\varepsilon^2)$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$として、平均化方程式を解くと、
\[ r(T) \approx \frac{3 \pi a}{4 a - (4 a - 3 \pi) e^{-\frac{T}{2}} } + \mathcal{O}(\varepsilon), \ \ \phi_0 = \mathcal{O}(\varepsilon) \]となるので、
\[ x(t, \varepsilon) \approx \frac{3 \pi a}{4 a - (4 a - 3 \pi) e^{-\frac{\varepsilon t}{2}} } \cos t + \mathcal{O}( \varepsilon ) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 14:46:51
|
|
|
P.259の問題番号「7.6.9」
に対する解答
$\ddot{x}+x+\varepsilon h(x, \dot{x}) = 0, \ \ h(x,\dot{x}) = (x^2-1) \dot{x}^3$
解)この系では$h=-r^3 \sin^3 \theta ( r^2 \cos^2 \theta - 1 )$となるので、平均化方程式は
\[ r' = \langle h \sin \theta \rangle = -r^5 \langle \sin^4 \theta \cos^2 \theta \rangle + r^3 \langle \sin^4 \theta \rangle = \frac{3}{8}r^3 - \frac{1}{16} r^5, \\
r \phi' = \langle h \cos \theta \rangle = -r^5 \langle \sin^3 \theta \cos^3 \theta \rangle + r^3 \langle \sin^3 \theta \cos \theta \rangle = 0 \]となる。
\[ r' = \frac{1}{16} r^3 (6-r^2) \]は$r \geq 0$の半直線上のベクトル場に対応すると見なせるので、$r^* = 0$は不安定固定点、$r^*= \frac{3 \pi}{4}$は安定固定点となる。一方、$\phi' = 0$より、ある定数$\phi_0$に対して$\phi(T) \equiv \phi_0$となる。したがって、長時間挙動は
\[ x(t) \to \sqrt{6} \cos ( t+ \phi_0 ) + \mathcal{O}(\varepsilon) \]となり、$x(t)$は半径$\sqrt{6} + \mathcal{O}(\varepsilon)$の安定なリミットサイクルに近づいていく。つまり、振幅は$\sqrt{6} + \mathcal{O}(\varepsilon)$、振動数は$1 + \mathcal{O}(\varepsilon^2)$となる。
初期条件$x(0)=a, \ \ \dot{x}(0) = 0$として、平均化方程式を解くと、
\[ \frac{r^2-6}{r^2} e^{\frac{6}{r^2}} = \frac{a^2-6}{a^2} e^{\frac{6}{a^2}} e^{-\frac{9}{2} T }, \ \ \phi_0 = \mathcal{O}(\varepsilon) \]となる。
投稿者:goodbook
投稿日時:2021-02-27 14:56:06
|
|





