|
P.259の問題番号「7.6.10」
に対する解答
\[ \sin \theta \cos^2 \theta = \frac{1}{4} [ \sin \theta + \sin 3 \theta ] \]解)
\[ \begin{align}
\sin \theta \cos^2 \theta &= \frac{e^{i \theta} - e^{-i \theta}}{2i} \left( \frac{e^{i \theta} + e^{-i \theta}}{2} \right)^2 \\
&= \frac{e^{i \theta} - e^{-i \theta}}{2i} \cdot \frac{e^{2 i \theta} + 2 + e^{-2 i \theta}}{4} \\
&= \frac{ e^{3 i \theta} + e^{i \theta} - e^{-i \theta} - e^{- 3 i \theta} }{8i} \\
&= \frac{1}{4} \left[ \frac{e^{i \theta} - e^{-i \theta}}{2i} + \frac{e^{3i \theta} - e^{-3i \theta}}{2i} \right] \\
&= \frac{1}{4} [ \sin \theta + \sin 3 \theta ]
\end{align}
\]
投稿者:goodbook
投稿日時:2021-02-28 06:51:33
|
|
|
P.259の問題番号「7.6.11」
に対する解答
\[ \partial_{\tau \tau} x_1 + x_1 = - \frac{1}{4} r^3 \sin 3(\tau + \phi) \]解)$x_1(\tau) = A \sin 3(\tau + \phi)$とおくと、
\[ \partial_{\tau \tau} x_1 + x_1 = -8 A \sin 3(\tau + \phi) \]となるので、
\[ x_1(\tau) = \frac{1}{32} r^3 \sin 3(\tau + \phi) \]が得られる。初期条件$x(0)=2, \ \ \dot{x}(0) = 0$とすると、$r(T)=2, \ \ \phi(T)=0$となるので、
\[ x_1(\tau) = \frac{1}{4} \sin 3 \tau \]となる。
投稿者:goodbook
投稿日時:2021-02-28 07:04:29
|
|
|
P.259の問題番号「7.6.12」
に対する解答
(a)\[
\begin{align}
\langle \cos k \theta \sin m \theta \rangle
&= \frac{1}{2 \pi} \int_0^{2 \pi} \cos k \theta \sin m \theta d \theta \\
&= \frac{1}{2 \pi} \int_0^{2 \pi} \frac{1}{2} [ \sin (k+m) \theta - \sin (k-m) \theta ] d \theta
\end{align}
\]ここで、$k \neq m$のとき、
\[ \langle \cos k \theta \sin m \theta \rangle = \frac{1}{4 \pi} \left[ -\frac{1}{k+m} \cos (k+m) \theta + \frac{1}{k-m} \cos (k-m) \theta \right]_0^{2 \pi} = 0 \]となり、$k = m$のとき
\[ \langle \cos k \theta \sin m \theta \rangle = \frac{1}{4 \pi} \left[ -\frac{1}{2k} \cos (2k) \theta \right]_0^{2 \pi} = 0 \]となる。
\[
\begin{align}
\langle \cos k \theta \cos m \theta \rangle
&= \frac{1}{2 \pi} \int_0^{2 \pi} \cos k \theta \cos m \theta d \theta \\
&= \frac{1}{2 \pi} \int_0^{2 \pi} \frac{1}{2} [ \cos (k+m) \theta + \cos (k-m) \theta ] d \theta \\
&= \frac{1}{4 \pi} \left[ \frac{1}{k+m} \sin (k+m) \theta + \frac{1}{k-m} \sin (k-m) \theta \right]_0^{2 \pi} \\
&= 0
\end{align}
\] \[
\begin{align}
\langle \sin k \theta \sin m \theta \rangle
&= \frac{1}{2 \pi} \int_0^{2 \pi} \sin k \theta \sin m \theta d \theta \\
&= \frac{1}{2 \pi} \int_0^{2 \pi} \frac{1}{2} [ \cos (k-m) \theta - \cos (k+m) \theta ] d \theta \\
&= \frac{1}{4 \pi} \left[ \frac{1}{k-m} \sin (k-m) \theta - \frac{1}{k+m} \sin (k+m) \theta \right]_0^{2 \pi} \\
&= 0
\end{align}
\] \[
\begin{align}
\langle \cos^2 k \theta \rangle
&= \frac{1}{2 \pi} \int_0^{2 \pi} \cos^2 k \theta d \theta \\
&= \frac{1}{2 \pi} \int_0^{2 \pi} \frac{1}{2} [ 1 + \cos 2k \theta ] d \theta \\
&= \frac{1}{4 \pi} \left[ \theta + \frac{1}{2k} \sin 2k \theta \right]_0^{2 \pi} \\
&= \frac{1}{2}
\end{align}
\] \[
\begin{align}
\langle \sin^2 k \theta \rangle
&= \frac{1}{2 \pi} \int_0^{2 \pi} \sin^2 k \theta d \theta \\
&= \frac{1}{2 \pi} \int_0^{2 \pi} \frac{1}{2} [ 1 - \cos 2k \theta ] d \theta \\
&= \frac{1}{4 \pi} \left[ \theta - \frac{1}{2k} \sin 2k \theta \right]_0^{2 \pi} \\
&= \frac{1}{2}
\end{align}
\]
投稿者:goodbook
投稿日時:2021-02-28 07:39:03
|
|
|
P.259の問題番号「7.6.13」
に対する解答
ダフィン振動子$\ddot{x}+x+\varepsilon x^3=0, \ \ 0 < \varepsilon \ll 1, \ \ x(0)=a, \ \ \dot{x}(0)=0$
(a)ダフィン方程式をベクトル場として表すと、
$\dot{x}=y, \ \ \dot{y}=-x-\varepsilon x^3$
と書ける。また、この系のエネルギーは
\[ E= \frac{1}{2} \dot{x}^2 + \frac{1}{2} x^2 + \frac{1}{4} \varepsilon x^4 = \frac{1}{2} y^2 + \frac{1}{2} x^2 + \frac{1}{4} \varepsilon x^4 \]となり、初期条件$x(0)=a, \ \ \dot{x}(0)=0$を考慮すると、
\[ \frac{1}{2} y^2 + \frac{1}{2} x^2 + \frac{1}{4} \varepsilon x^4 = \frac{1}{2} a^2 + \frac{1}{4} \varepsilon a^4 \]が得られる。
次に、ベクトル場を極座標で
$x= r \cos \theta, \ \ y= r \sin \theta$
と表すと、エネルギーの式は
\[ \frac{1}{2} r^2 + \frac{1}{4} \varepsilon r^4 \cos^4 \theta = \frac{1}{2} a^2 + \frac{1}{4} \varepsilon a^4 \]となり、この式から、
\[ r^2 = \frac{-1 + \sqrt{ 1 + \varepsilon \cos^4 \theta ( 2a^2 + \varepsilon a^4 ) } }{\varepsilon \cos^4 \theta } \]を得る。また、
\[ \frac{d \theta}{d t} = \frac{x \dot{y} - y \dot{x} }{r^2} = -(1 + \varepsilon r^2 \cos^4 \theta ) \]となるので、周期$T(\varepsilon)$は
\[ \begin{align}
T(\varepsilon) &= \int^T dt = \int_0^{2 \pi} \frac{dt}{d \theta} d \theta \\
&= \int_0^{2 \pi} \frac{d \theta}{1 + \varepsilon r^2 \cos^4 \theta} \\
&= \int_0^{2 \pi} \frac{d \theta}{\sqrt{ 1 + \varepsilon \cos^4 \theta ( 2a^2 + \varepsilon a^4 ) }}
\end{align}
\]となる。
投稿者:goodbook
投稿日時:2021-03-02 04:30:37
|
|
|
P.260の問題番号「7.6.14」
に対する解答
系$\ddot{x} + \varepsilon \dot{x}^3 + x = 0$
(a) この系では$h=-r^3 \sin^3 \theta$であるので、平均化方程式は
\[ \begin{align}
r' &= \langle h \sin \theta \rangle = -r^3 \langle \sin^4 \theta \rangle = - \frac{3}{8} r^3 \\
r \phi' &= \langle h \cos \theta \rangle = -r^3 \langle \sin^3 \theta \cos \theta \rangle = 0
\end{align}
\]となる。
(b) 初期条件$x(0)=a, \ \ \dot{x}(0)=0$の場合に平均化方程式を解くと、
\[ r(T) = \frac{2a}{\sqrt{3 a^2 T + 4}}, \ \ \phi(T)=0 \]となるので、
\[ x(t, \varepsilon) = \frac{2a}{\sqrt{3 a^2 \varepsilon t + 4}} \cos t + \mathcal{O}(\varepsilon) \]を得る。
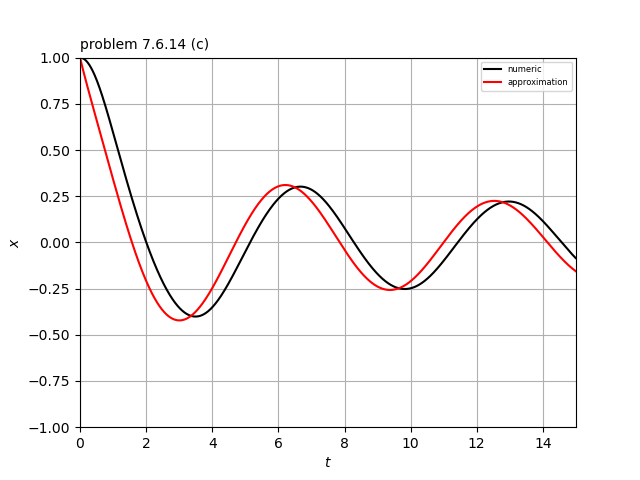
(c) $\ddot{x} + \varepsilon \dot{x}^3 + x = 0$を$a=1, \ \ \varepsilon=2$のときにプロットしたものは添付図のようになる。
投稿者:goodbook
投稿日時:2021-03-02 05:45:15
|
|
|
P.260の問題番号「7.6.15」
に対する解答
系$\ddot{x} + \sin x = 0$
(a) 小振幅の場合、
\[ \sin x \approx x -\frac{1}{6} x^3 \]とおいて、$\frac{1}{6}x^3$を微小摂動と考えることができる。このとき、$h=r^3 \cos^3 \theta$とおくと、平均化方程式は
\[ \begin{align}
r' &= \langle h \sin \theta \rangle = r^3 \langle \sin \theta \cos^3 \theta \rangle = 0 \\
r \phi' &= \langle h \cos \theta \rangle = r^3 \langle \cos^4 \theta \rangle = \frac{3}{8} r^3
\end{align}
\]となる。よって、$a$をある定数として$r(T) \equiv a, \ \ \phi' = \frac{3}{8} a^2$と求まる。したがって、振動数$\omega$は
\[ \omega \approx 1+ \varepsilon \phi' = 1 + \left( -\frac{1}{6} \right) \cdot \frac{3}{8} a^2 = 1 - \frac{1}{16} a^2 \]で与えられることがわかる。
(b) $T=2 \pi/ \omega$で、$a\ll1$であることを考慮すると、
\[ T = 2\pi \left[ 1 - \frac{1}{16} a^2 \right]^{-1} \approx 2 \pi \left( 1+ \frac{1}{16} a^2 \right) \]となるので、$\omega$の表式は演習問題6.7.4で得られた結果と整合することがわかる。
投稿者:goodbook
投稿日時:2021-03-03 04:51:40
|
|
|
P.260の問題番号「7.6.16」
に対する解答
ファン・デル・ポール振動子$\ddot{x} + \varepsilon \dot{x} (x^2-1) +x =0$の$\varepsilon \ll 1$の極限におけるほぼ円形のリミットサイクルの半径
解)この系をベクトル場$\boldsymbol{v}=\dot{\boldsymbol{x}} = (\dot{x}, \dot{y})$で表すと、
$\dot{x}=y, \ \ \dot{y} = -x - \varepsilon y (x^2-1)$
となる。
$\varepsilon \ll 1$の極限において、この系のリミットサイクルを原点を中心とするほぼ円の形をしたものであるとすると、
\[ \boldsymbol{v} \cdot \boldsymbol{n} \approx 0 \]とすることができる。よって、閉軌道$C$をリミットサイクル上にとると、
\[ \oint_C \boldsymbol{v} \cdot \boldsymbol{n} dl \approx 0 \]とみなすことができる。一方、
\[ \nabla \cdot \boldsymbol{v} = - \varepsilon (x^2-1) \]となるので、リミットサイクルの円の半径を$a$とすると、
\[ \begin{align}
\iint_A \nabla \cdot \boldsymbol{v} dA &= - \varepsilon \iint_A (x^2-1) dA \\
&= - \varepsilon \int_0^a \int_0^{2 \pi} ( r^2 \cos^2 \theta -1 ) rdrd \theta \\
&= -2 \pi \varepsilon \left[ \frac{1}{8} a^4 - \frac{1}{2} a^2 \right]
\end{align}
\]となる。したがって、グリーンの定理より
\[ -2 \pi \varepsilon \left[ \frac{1}{8} a^4 - \frac{1}{2} a^2 \right] \approx 0 \]となり、$a \approx 2$が得られる。
投稿者:goodbook
投稿日時:2021-03-04 04:11:08
|
|
|
P.260の問題番号「7.6.17」
に対する解答
子供のブランコ遊びの単純なモデル$\ddot{x} + (1 + \varepsilon \gamma + \varepsilon \cos 2t ) \sin x = 0, \ \ (0< \varepsilon \ll 1 )$
(a) 微小な$x$の場合を考え、$\ddot{x} + (1 + \varepsilon \gamma + \varepsilon \cos 2t ) x = 0$に置き換える。
このとき、$h = (\gamma + \cos 2t) r \cos \theta$とおくと、平均化方程式は
\[ \begin{align}
r' &= \langle h \sin \theta \rangle = r ( \gamma \langle \sin \theta \cos \theta \rangle + \langle \cos 2t \sin \theta \cos \theta \rangle ) = \frac{1}{4} r \sin 2 \phi \\
r \phi' &= \langle h \cos \theta \rangle = r ( \gamma \langle \cos^2 \theta \rangle + \langle \cos 2t \cos^2 \theta \rangle ) = \frac{1}{2} r \left( \gamma + \frac{1}{2} \cos 2 \phi \right)
\end{align}
\]となる。ここで、
\[ \langle \cos 2t \cos^2 \theta \rangle = \frac{1}{4} \cos 2 \phi \]を用いた。
(b) まず$\phi$についての方程式を解く。
\[ \gamma + \frac{1}{2} \cos 2 \phi = \gamma - \frac{1}{2} + \cos^2 \phi \]となるので、$\gamma^2-\frac{1}{4} < 0$のとき、
\[ \int \left[ \gamma - \frac{1}{2} + \cos^2 \phi \right]^{-1} d \phi = \frac{1}{2 \sqrt{\frac{1}{4} - \gamma^2}} \ln \left| \frac{ \sqrt{ \frac{1}{4} - \gamma^2 } \tan \phi + \gamma + \frac{1}{2} }{ \sqrt{ \frac{1}{4} - \gamma^2 } \tan \phi - \gamma - \frac{1}{2} } \right| = \frac{1}{2} + C \]となる。つまり、
\[ \tan \phi = \sqrt{ \frac{ \frac{1}{2} + \gamma }{ \frac{1}{2} - \gamma } } \cdot \frac{ 1 - A e^{-\sqrt{\frac{1}{4}-\gamma^2}T} }{ 1 + A e^{-\sqrt{\frac{1}{4}-\gamma^2}T} } \]となる。ここで、$A$は積分定数。
次に、$r$についての方程式を解くことを考える。(ヒントにある通り)$r$が$0$に近い場合、$\phi' \gg r'$であり、$\phi$は相対的により速く固定点に近づいていくので、
\[ \tan \phi \approx \sqrt{ \frac{ \frac{1}{2} + \gamma }{ \frac{1}{2} - \gamma } } \]と置くことができる。
\[ \sin 2 \phi = \frac{ 2 \tan \phi }{ 1 + \tan^2 \phi } \approx 2 \sqrt{ \frac{1}{4} - \gamma^2 } \]となるので、$r$の方程式は
\[ r(T) \approx r_0 e^{\frac{1}{2} \sqrt{\frac{1}{4} - \gamma^2} T } \]のようになる。
まとめると、$\gamma_c = \frac{1}{2}$として、$|\gamma|<\gamma_c$であるとき、固定点は不安定であり、指数関数的に成長する振動が生じることがわかる。
(c) (b)の結果より、成長率$k$は
\[ k= \frac{1}{2} \sqrt{ \frac{1}{4} - \gamma^2 } \]となる。
投稿者:goodbook
投稿日時:2021-03-06 08:32:50
|
|
|
P.261の問題番号「7.6.18」
に対する解答
マシュー方程式(Mathieu equation)$\ddot{x} + (a + \varepsilon \cos t ) x = 0, \ \ a \approx 1$
解)$\tau = t$として$\tau$を速い時間とし、$T = \varepsilon^2 t$を遅い時間とすると、
\[ \dot{x} = \frac{\partial x}{\partial t} = \frac{\partial x}{\partial \tau} + \frac{\partial x}{\partial T} \frac{\partial T}{ \partial t} = \partial_{\tau} x + \varepsilon^2 \partial_T x \]となる。また、
\[ x(t,\varepsilon) = x_0(\tau, T ) + \varepsilon x_1(\tau, T) + \varepsilon^2 x_2(\tau, T) + \mathcal{O}(\varepsilon^3) \]とおくと、
\[ \dot{x} = \partial_{\tau} x_0 + \varepsilon \partial_{\tau} x_1 + \varepsilon^2 ( \partial_{\tau} x_2 + \partial_T x_0 ) + \mathcal{O}(\varepsilon^3), \\
\ddot{x} = \partial_{\tau \tau} x_0 + \varepsilon \partial_{\tau \tau} x_1 + \varepsilon^2 ( \partial_{\tau \tau} x_2 + 2 \partial_{T \tau} x_0 ) + \mathcal{O}(\varepsilon^3) \]となる。さらに、
\[ a = 1 + \varepsilon a_1 + \varepsilon^2 a_2 + \mathcal{O}(\varepsilon^3) \]とおき、上記の式をマシュー方程式に代入して$\varepsilon$のべき順に整理すると、
\[ \begin{align}
\mathcal{O}(1) \ &: \ \partial_{\tau \tau} x_0 + x_0 = 0 \\
\mathcal{O}(\varepsilon) \ &: \ \partial_{\tau \tau} x_1 + x_1 + (a_1 + \cos t ) x_0 = 0 \\
\mathcal{O}(\varepsilon^2) \ &: \ \partial_{\tau \tau} x_2 + x_2 + (a_1 + \cos t ) x_1 + 2 \partial_{T \tau} x_0 + a_2 x_0 = 0
\end{align} \]となる。
投稿者:goodbook
投稿日時:2021-03-11 07:49:52
|
|
|
P.261の問題番号「7.6.19」
に対する解答
ダフィン方程式$\ddot{x}+x+\varepsilon x^3 = 0, \ \ 0< \varepsilon \ll 1, \ \ x(0)=a, \ \ \dot{x}(0)=0$
(a) $\tau = \omega t$とおくと、
\[ \dot{x} = \frac{dx}{dt} = \frac{d \tau}{d t} \frac{dx}{d \tau} = \omega x', \ \ \ddot{x} = \omega^2 x'' \]となる。したがって、ダフィン方程式は
\[ \omega^2 x'' + x + \varepsilon x^3 = 0 \]となる。
(b) $x(\tau, \varepsilon) = x_0(\tau) + \varepsilon x_1(\tau) + \mathcal{O}(\varepsilon^2), \ \ \omega = 1 + \varepsilon \omega_1 + \mathcal{O}(\varepsilon^2)$とおき、ダフィン方程式に代入すると、
\[ (1 + \varepsilon \omega_1)^2( x_0'' + \varepsilon x_1'' ) + (x_0 + \varepsilon x_1) + \varepsilon (x_0 + \varepsilon x_1)^3 + \mathcal{O}(\varepsilon^2) = 0 \]となるので、$\varepsilon$のべきごとに整理すると、
\[ \begin{align}
\mathcal{O}(1) \ &: \ x_0'' + x_0 = 0 \\
\mathcal{O}(\varepsilon) \ &: \ x_1'' + x_1 = -2 \omega_1 x_0'' - x_0^3
\end{align}
\]が得られる。
(c) 初期条件は
\[ \begin{align}
x(0) &= x_0(0) + \varepsilon x_1(0) + \varepsilon^2 x_2(0) + \mathcal{O}(\varepsilon^3) = a \\
\dot{x}(0) &= \dot{x}_0(0) + \varepsilon \dot{x}_1(0) + \varepsilon^2 \dot{x}_2(0) + \mathcal{O}(\varepsilon^3) = 0
\end{align}
\]となるので、$\varepsilon$のべきごとに整理すれば、$x_0(0)=a, \ \dot{x}_0(0)=0$、およびすべての$k>0$に対して、$x_k(0)=\dot{x}_k(0)=0$が得られる。
(d) $\mathcal{O}(1)$の方程式の一般解は
\[ x_0(\tau) = A \sin \tau + B \cos \tau \]であるので、初期条件$x_0(0)=a, \ \dot{x}_0(0)=0$から
\[ x_0(\tau) = a \cos \tau \]が得られる。
(e) $x_0'' = - a \cos \tau$と
\[ \cos^3 \tau = \frac{3}{4} \cos \tau + \frac{1}{4} \cos 3 \tau \]を用いると、$\mathcal{O}(\varepsilon)$の方程式は
\[ x_1'' + x_1 = \left( 2 \omega_1 a - \frac{3}{4} a^3 \right) \cos \tau - \frac{1}{4} a^3 \cos 3 \tau \]となる。したがって、永年項を回避するために、$\omega_1=\frac{3}{8} a^2$が必要となる。
(f) $\mathcal{O}(\varepsilon)$の方程式を解くと、
\[ x_1(\tau) = \frac{1}{32} a^3 \cos 3 \tau \]が得られる。
投稿者:goodbook
投稿日時:2021-03-12 06:36:43
|
|





