ストロガッツ非線形ダイナミクスとカオス　の読書会ページ

P.262の問題番号「7.6.21」 に対する解答

解）$\tau = \omega t$とおくと、方程式は
\[ \omega^2 x'' + \varepsilon \omega (x^2-1) x' + x = 0 \]となる。$x(t, \varepsilon) = x_0(t) + \varepsilon x_1(t) + \varepsilon^2 x_2(t) + \mathcal{O}(\varepsilon^3), \ \ \omega = 1 + \varepsilon \omega_1 + \varepsilon^2 \omega_2 + \mathcal{O}(\varepsilon^3)$とおき、方程式に代入すると、
\[ (1 + \varepsilon \omega_1 + \varepsilon^2 \omega_2)^2 ( x_0'' + \varepsilon x_1'' + \varepsilon^2 x_2'') \\
+ \varepsilon (1 + \varepsilon \omega_1) \{ ( x_0 + \varepsilon x_1 )^2 -1 \}(x_0' + \varepsilon x_1' ) + (x_0 + \varepsilon x_1 + \varepsilon^2 x_2 ) + \mathcal{O}(\varepsilon^3) = 0 \]となるので、$\varepsilon$のべきごとに整理すると、
\[ \begin{align}
\mathcal{O}(1) \ &: \ x_0'' + x_0 = 0 \\
\mathcal{O}(\varepsilon) \ &: \ x_1'' + x_1 + 2 \omega_1 x_0'' + (x_0^2 - 1 ) x_0' = 0 \\
\mathcal{O}(\varepsilon^2) \ &: \ x_2'' + x_2 + ( \omega_1^2 + 2 \omega_2) x_0'' + 2 \omega_1 x_1'' + (x_0^2 - 1 ) (\omega_1 x_0' + x_1' ) + 2 x_0 x_0' x_1 = 0
\end{align}
\]が得られる。$\mathcal{O}(1)$の方程式から
\[ x_0(\tau) = r_0 \cos (\tau + \phi_0) \]が得られる。次に、$\mathcal{O}(\varepsilon)$の方程式は、
\[ x_1'' + x_1 = 2 \omega_1 r_0 \cos (\tau + \phi_0) + \left( \frac{r_0^3}{4} - r_0 \right) \sin (\tau + \phi_0) + \frac{r_0^3}{4} \sin 3(\tau+\phi_0) \]となる。この式から永年項を回避するために、
\[ \omega_1 = 0, r_0 = 2 \]が得られる。また、このとき、
\[ x_1(\tau) = r_1 \cos (\tau + \phi_1) - \frac{1}{4} \sin 3(\tau+ \phi_0) \]となる。さらに、$\mathcal{O}(\varepsilon^2)$の方程式は、
\[ \begin{align}
x_2'' + x_2 &= \left( 4 \omega_2 + r_1 \sin( \phi_0 - \phi_1) + \frac{1}{4} \right) \cos(\tau+ \phi_0) \\
&+ r_1 ( 1+ \cos (\phi_0-\phi_1) ) \sin (\tau + \phi_0) \\
&+ 3 \left( - r_1 \sin (\phi_0 - \phi_1) + \frac{1}{4} \right) \cos 3(\tau+\phi_0) \\
&+ 3r_1 \cos(\phi_0 - \phi_1) \sin 3 (\tau + \phi_0) + \frac{5}{4} \cos 5(\tau+\phi_0)
\end{align} \]となるので、永年項を回避するために、
\[ \omega_2 = - \frac{1}{16} \]が得られる。したがって、リミットサイクルの振動数は、
\[ \omega = 1 - \frac{1}{16} \varepsilon^2 + \mathcal{O}(\varepsilon^3) \]となる。

投稿者：goodbook 投稿日時：2021-03-13 12:05:31

P.262の問題番号「7.6.23」 に対する解答

系$\ddot{x} - \varepsilon x \dot{x} + x = 0$
解）$\tau = \omega t$とおくと、方程式は
\[ \omega^2 x'' - \varepsilon x x' + x = 0 \]となる。$x(t, \varepsilon) = x_0(t) + \varepsilon x_1(t) + \varepsilon^2 x_2(t) + \mathcal{O}(\varepsilon^3), \ \ \omega = 1 + \varepsilon \omega_1 + \varepsilon^2 \omega_2 + \mathcal{O}(\varepsilon^3)$とおき、方程式に代入すると、
\[ (1 + \varepsilon \omega_1 + \varepsilon^2 \omega_2)^2 ( x_0'' + \varepsilon x_1'' + \varepsilon^2 x_2'') \\
- \varepsilon (1 + \varepsilon \omega_1) ( x_0 + \varepsilon x_1 ) (x_0' + \varepsilon x_1' ) + (x_0 + \varepsilon x_1 + \varepsilon^2 x_2 ) + \mathcal{O}(\varepsilon^3) = 0 \]となるので、$\varepsilon$のべきごとに整理すると、
\[ \begin{align}
\mathcal{O}(1) \ &: \ x_0'' + x_0 = 0 \\
\mathcal{O}(\varepsilon) \ &: \ x_1'' + x_1 + 2 \omega_1 x_0'' - x_0 x_0' = 0 \\
\mathcal{O}(\varepsilon^2) \ &: \ x_2'' + x_2 + ( \omega_1^2 + 2 \omega_2) x_0'' + 2 \omega_1 x_1'' - \omega_1 x_0 x_0' - x_0' x_1 - x_0 x_1' = 0
\end{align}
\]が得られる。$\mathcal{O}(1)$の方程式から
\[ x_0(\tau) = r_0 \cos (\tau + \phi_0) \]が得られる。次に、$\mathcal{O}(\varepsilon)$の方程式は、
\[ x_1'' + x_1 = 2 \omega_1 r_0 \cos (\tau + \phi_0) - \frac{r_0^2}{2} \sin 2 (\tau + \phi_0) \]となる。この式から永年項を回避するために、
\[ \omega_1 = 0 \]が得られる。また、このとき、
\[ x_1(\tau) = r_1 \cos (\tau + \phi_1) + \frac{r_0^2}{6} \sin 2(\tau+ \phi_0) \]となる。さらに、$\mathcal{O}(\varepsilon^2)$の方程式は、
\[ x_2'' + x_2 = \left( 2 \omega_2 r_0 + \frac{r_0^3}{12} \right) \cos(\tau+ \phi_0) + \frac{r_0^3}{4} \cos 3(\tau + \phi_0) -r_0 r_1 \sin (2 \tau + \phi_0 + \phi_1 ) \]となるので、永年項を回避するために、
\[ \omega_2 = - \frac{r_0^2}{24} \]が得られる。したがって、振幅と振動数の間の近似的な関係式は、
\[ \omega \approx 1 - \frac{1}{24} \varepsilon^2 r_0^2 \]となる。

投稿者：goodbook 投稿日時：2021-03-14 06:12:48

P.262の問題番号「7.6.25」 に対する解答

系$\ddot{x} + x + \varepsilon h(x,\dot{x},t)=0$
(a) 変数変換$x(t) = r(t) \cos (t+\phi(t)), \ \ \dot{x}(t) = - r(t) \sin (t + \phi(t))$とおいたとき、$y(t)=-\dot{x}(t)$とすると、系は
\[ \dot{x}=-y, \ \ \dot{y} = x + \varepsilon h \]と表すことができ、変数変換
\[ x = r \cos (t+\phi), \ \ y=r \sin (t + \phi) \]は極座標への変換とみなすことができる。したがって、
\[ r \dot{r} = x \dot{x} + y \dot{y} = \varepsilon h y = \varepsilon h r \sin (t+\phi) \]から、
\[ \dot{r} = \varepsilon h \sin (t + \phi) \]が得られる。また、
\[ r^2 (1 + \dot{\phi}) = x \dot{y} - y \dot{x} = r^2 + \varepsilon h x = r^2 + \varepsilon h r \cos (t+\phi) \]から
\[ r \dot{\phi} = \varepsilon h \cos (t+ \phi) \]が得られる。

(b) 移動平均$\langle r \rangle$は
\[ \langle r \rangle = \frac{1}{2 \pi} \int_{t-\pi}^{t+\pi} r(\tau) d \tau = \frac{1}{2 \pi} \int_{-\pi}^{\pi} r(t+\tau) d \tau \]と表せる。したがって、
\[ \begin{align}
\frac{ d \langle r \rangle}{d t} &= \frac{d}{d t} \left[ \frac{1}{2 \pi} \int_{-\pi}^{\pi} r(t+\tau) d \tau \right] \\
&= \frac{1}{2 \pi} \int_{-\pi}^{\pi} \frac{d}{dt} r(t+\tau) d \tau \\
&= \frac{1}{2 \pi} \int_{-\pi}^{\pi} \frac{d r(t+\tau)}{d(t+\tau)} \frac{d(t+\tau)}{dt} d \tau \\
&= \frac{1}{2 \pi} \int_{-\pi}^{\pi} \dot{r}(t+\tau) d \tau \\
&= \langle \frac{dr}{dt} \rangle
\end{align} \]となる。

(c) (b)の結果より
\[ \begin{align}
\frac{ d \langle r \rangle}{d t} &= \langle \dot{r} \rangle = \langle \varepsilon h [x(t), \dot{x}(t), t] \sin(t+\phi(t)) \rangle \\
&= \varepsilon \langle h [r \cos(t+\phi), -r \sin(t+\phi), t] \sin(t+\phi(t)) \rangle
\end{align} \]となる。

投稿者：goodbook 投稿日時：2021-03-18 06:02:03

P.311の問題番号「8.1.1」 に対する解答

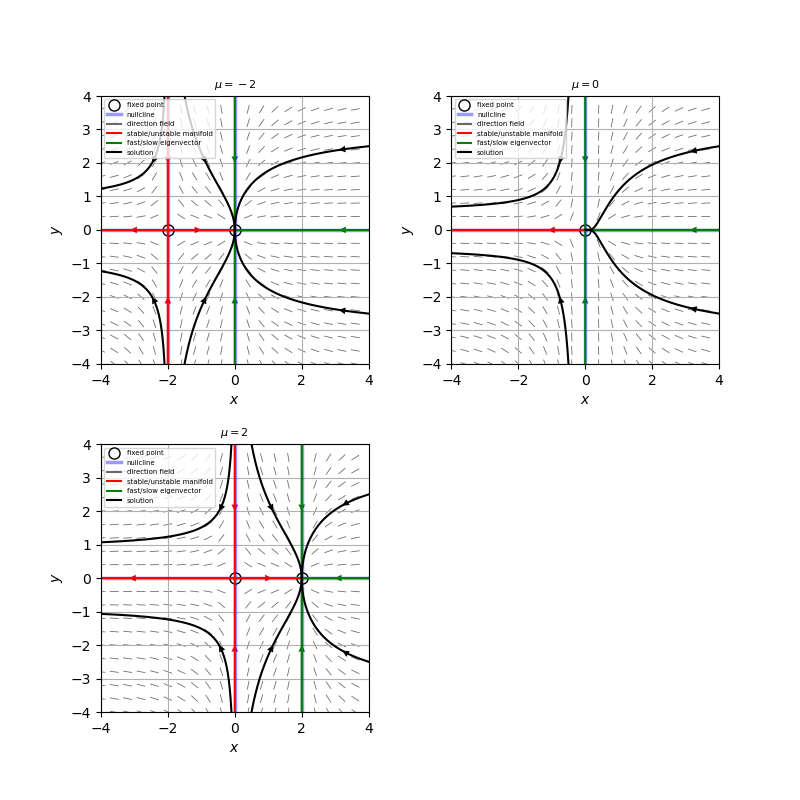
(a) $\dot{x} = \mu x - x^2, \ \ \dot{y} = -y$（トランスクリティカル分岐）
解）この系の固定点は$(0,0), \ \ (\mu, 0)$の2点。各点のヤコビ行列は
\[ (0,0) \ : \ A = \begin{pmatrix} \mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=\mu-1, \ \ \Delta = -\mu, \ \ \tau^2 - 4 \Delta = (\mu+1)^2 \geq 0 \\
(\mu, 0) \ : \ A = \begin{pmatrix} -\mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=-\mu-1, \ \ \Delta = \mu, \ \ \tau^2 - 4 \Delta = (\mu-1)^2 \geq 0\]したがって、$\mu < 0$のとき、$(0,0)$は安定ノード、$(\mu,0)$はサドルとなる。$\mu$が増加するにつれて、$(\mu,0)$は原点に近づき、$\mu=0$でこれらは一致する。このとき、原点は孤立していない固定点と予想されるが、実際は$x<0$の領域でサドルのふるまいをし、$x>0$の領域で安定ノードのふるまいをする。さらに、$\mu>0$では$(0,0)$がサドル、$(\mu,0)$が安定ノードとなる。

投稿者：goodbook 投稿日時：2021-03-21 16:12:40

P.312の問題番号「8.1.3」 に対する解答

系$\dot{x} = \mu x - x^2, \ \ \dot{y}=-y$
解）この系の固定点は$(0,0), \ \ (\mu, 0)$の2点で、各点のヤコビ行列は
\[ (0,0) \ : \ A = \begin{pmatrix} \mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=\mu-1, \ \ \Delta = -\mu, \ \ \tau^2 - 4 \Delta = (\mu+1)^2 \geq 0 \\
(\mu, 0) \ : \ A = \begin{pmatrix} -\mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=-\mu-1, \ \ \Delta = \mu, \ \ \tau^2 - 4 \Delta = (\mu-1)^2 \geq 0\]となる。このとき、各固定点での固有値は
\[ (0,0) \ : \ \lambda = \mu, \ \ -1, \ \ \ \ (\mu,0) \ : \ \lambda = -\mu, \ \ -1 \]であるので、それぞれの固定点の固有値のうち１つが$\mu \to 0$で$0$に近づくことがわかる。

投稿者：goodbook 投稿日時：2021-03-22 05:02:37