|
P.312の問題番号「8.1.4」
に対する解答
系$\dot{x} = \mu x + x^3, \ \ \dot{y}=-y$
解)$\mu<0$のとき、この系の固定点は$(0,0), \ \ (\pm \sqrt{-\mu}, 0)$の3点で、各点のヤコビ行列は
\[ (0,0) \ : \ A = \begin{pmatrix} \mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=\mu-1, \ \ \Delta = -\mu, \ \ \tau^2 - 4 \Delta = (\mu+1)^2 \geq 0 \\
(\pm \sqrt{-\mu}, 0) \ : \ A = \begin{pmatrix} -2 \mu & 0 \\ 0 & -1 \end{pmatrix}, \ \ \tau=-2 \mu-1, \ \ \Delta = 2 \mu, \ \ \tau^2 - 4 \Delta = (2 \mu-1)^2 \geq 0\]となる。このとき、各固定点での固有値は
\[ (0,0) \ : \ \lambda = \mu, \ \ -1, \ \ \ \ (\pm \sqrt{-\mu},0) \ : \ \lambda = -2 \mu, \ \ -1 \]であるので、それぞれの固定点の固有値のうち1つが$\mu \to 0$で$0$に近づくことがわかる。
投稿者:goodbook
投稿日時:2021-03-22 05:04:03
|
|
|
P.312の問題番号「8.1.5」
に対する解答
系$\dot{x}=f(x,y), \ \ \dot{y}=g(x,y)$を考える。$(x^*, y^*)$をこの系の固定点とすると、ヤコビ行列は
\[ A = \begin{pmatrix} f_x & f_y \\ g_x & g_y \end{pmatrix} \]となる。ここで、
\[ f_x = \left. \frac{ \partial f }{ \partial x } \right|_{(x^*, y^*)}, \ \ f_y = \left. \frac{ \partial f }{ \partial y } \right|_{(x^*, y^*)}, \ \ g_x = \left. \frac{ \partial g }{ \partial x } \right|_{(x^*, y^*)}, \ \ g_y = \left. \frac{ \partial g }{ \partial y } \right|_{(x^*, y^*)} \]とおいた。行列$A$がゼロ固有値をもつとすると、
\[ \Delta = f_x g_y - f_y g_x =0 \]となり、ベクトル$(f_x,f_y)$と$(g_x, g_y)$はそれぞれ曲線$f(x,y)=0$と$g(x,y)=0$に対する点$(x^*, y^*)$での法線ベクトルであることを考慮すると、$f_x g_y - f_y g_x =0$は$(f_x,f_y)$と$(g_x, g_y)$の外積の大きさが$0$、すなわち、$(f_x,f_y)$と$(g_x, g_y)$は平行であることがわかる。これはゼロ固有値分岐点において、2つのヌルクライン$f(x,y)=0$と$g(x,y)=0$が互いに接していることを示す。
投稿者:goodbook
投稿日時:2021-03-23 05:27:47
|
|
|
P.312の問題番号「8.1.6」
に対する解答
系$\dot{x}=y-2x, \ \ \dot{y} = \mu + x^2 -y$
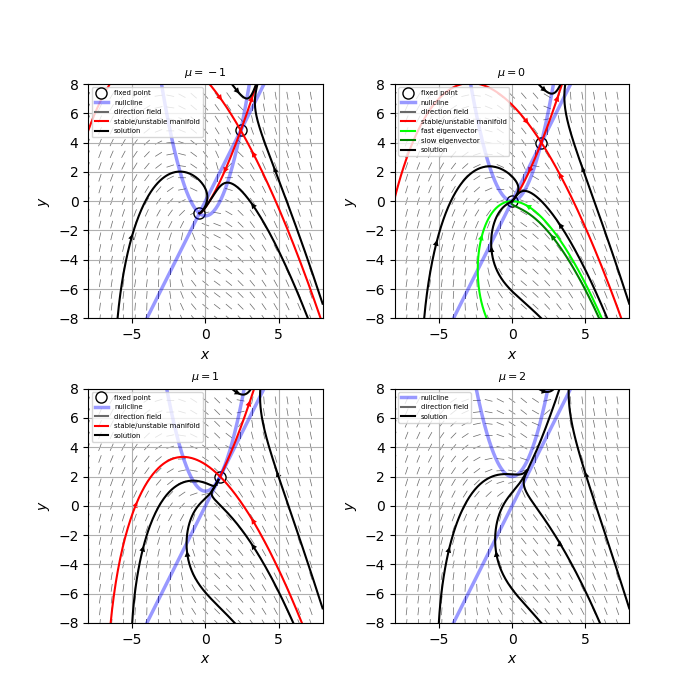
(a) ヌルクラインは添付図の青線。
(b)(c) $\mu<1$では2つの固定点$(1+\sqrt{1-\mu}, 2+2 \sqrt{1-\mu}), \ \ (1-\sqrt{1-\mu}, 2-2 \sqrt{1-\mu})$が存在する。各固定点のヤコビ行列を求めて分類すると、
\[ (1+\sqrt{1-\mu}, 2+2 \sqrt{1-\mu}) \ : \ A = \begin{pmatrix} -2 & 1 \\ 2+2 \sqrt{1-\mu} & -1 \end{pmatrix}, \\ \tau=-3, \ \ \Delta = -2 \sqrt{1-\mu}<0, \ \ \tau^2 - 4 \Delta = 9 + 8 \sqrt{1-\mu} \]となるので、サドルとなる。一方、
\[ (1-\sqrt{1-\mu}, 2-2 \sqrt{1-\mu}) \ : \ A = \begin{pmatrix} -2 & 1 \\ 2-2 \sqrt{1-\mu} & -1 \end{pmatrix}, \\ \tau=-3, \ \ \Delta = 2 \sqrt{1-\mu}>0, \ \ \tau^2 - 4 \Delta = 9 - 8 \sqrt{1-\mu} \]となるので、$\mu < -\frac{17}{64}$のとき安定スパイラル(添付図左上)、$-\frac{17}{64} \leq \mu <1$のとき安定ノード(添付図右上)となる。
$\mu$が増加するにつれて、サドルと安定ノードは互いに接近し、$\mu=1$で衝突(添付図左下)して最終的に$\mu>1$では消え失せる(添付図右下)。
投稿者:goodbook
投稿日時:2021-03-28 18:48:19
|
|
|
P.312の問題番号「8.1.7」
に対する解答
系$\dot{x}=y-ax, \ \ \dot{y} = -by + x/(1+x)$
解)この系では2つの固定点が存在する。これらの固定点を$A(0,0), \ \ B((1-ab)/ab, (1-ab)/b)$とおく。各固定点のヤコビ行列は
\[ \begin{align}
(0, 0) \ :& \ J = \begin{pmatrix} -a & 1 \\ 1 & -b \end{pmatrix}, \\
& \tau=-a-b, \ \ \Delta = ab-1, \ \ \tau^2 - 4 \Delta = (a-b)^2+4 >0 \\
\left( \frac{1-ab}{ab}, \frac{1-ab}{b} \right) \ :& \ J = \begin{pmatrix} -a & 1 \\ a^2 b^2 & -b \end{pmatrix}, \\
& \tau=-a-b, \ \ \Delta = ab - a^2 b^2, \ \ \tau^2 - 4 \Delta = (a-b)^2+4a^2b^2 \geq 0
\end{align} \]となる。したがって、$ab<0$のとき、固定点$A$、固定点$B$共にサドルとなる。$ab$が増加するにつれて固定点$B$は$x$軸の負の方向に離れていき、$ab=0$で無限遠となる。$0 <ab<1$となると、固定点$B$は固定点$A$に近づいていく。この間、固定点$A$はサドル、固定点$B$は$a>0,b>0$のとき安定ノード、$a<0,b<0$のとき不安定ノードとなる。$ab=1$で固定点$A, B$は互いに衝突し、$ab>1$になると、固定点$A$は$a>0,b>0$のとき安定ノード、$a<0,b<0$のとき不安定ノードとなり、固定点$B$はサドルとなる。つまり、$ab=1$でトランスクリティカル分岐を起こす。
投稿者:goodbook
投稿日時:2021-03-29 06:50:32
|
|
|
P.312の問題番号「8.1.8」
に対する解答
方程式
\[ \varepsilon \frac{d^2 \phi}{d \tau^2} = - \frac{d \phi}{d \tau} - \sin \phi + \gamma \sin \phi \cos \phi
\] (a) $\tau$での微分をプライムで表し、$\phi' = \theta$とおくと、
\[ \phi' = \theta, \ \ \varepsilon \theta' = - \theta - \sin \phi + \gamma \sin \phi \cos \phi \]が得られる。この系では、$n$を整数とすると、
$0<\gamma \leq 1$のとき、固定点$(2n\pi, 0), \ \ ((2n+1)\pi, 0)$をもち、
$\gamma > 1$のとき、固定点$(2n\pi, 0), \ \ ((2n+1)\pi, 0), \ \ (2n\pi \pm \alpha, 0)$をもつ。
ここで、$\alpha$は$\cos \alpha = \gamma^{-1}, \ \ 0 \leq \alpha < \pi/2$を満たす。
一方、各固定点でのヤコビ行列を求めて分類すると、それぞれ次のようになる。
\[ (2n\pi, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ -\varepsilon^{-1}(1-\gamma) & -\varepsilon^{-1} \end{pmatrix}, \\
\tau=-\varepsilon^{-1}, \ \ \Delta = \varepsilon^{-1}(1-\gamma), \ \ \tau^2 - 4 \Delta = \varepsilon^{-2}(1-4 \varepsilon + 4 \varepsilon \gamma) \]となり、$0<\gamma \leq 1$では安定な固定点、$\gamma > 1$ではサドルとなる。
\[ ((2n+1)\pi, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ \varepsilon^{-1}(1+\gamma) & -\varepsilon^{-1} \end{pmatrix}, \\
\tau=-\varepsilon^{-1}, \ \ \Delta = -\varepsilon^{-1}(1+\gamma) <0 , \ \ \tau^2 - 4 \Delta = \varepsilon^{-2}(1+4 \varepsilon + 4 \varepsilon \gamma) \]となり、常にサドルとなる。
\[ (2n\pi \pm \alpha, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ -\varepsilon^{-1}(\gamma-\gamma^{-1}) & -\varepsilon^{-1} \end{pmatrix}, \\
\tau=-\varepsilon^{-1}, \ \ \Delta = \varepsilon^{-1} (\gamma - \gamma^{-1}), \ \ \tau^2 - 4 \Delta = \varepsilon^{-2}(1-4 \varepsilon \gamma + 4 \varepsilon \gamma^{-1}) \]となり、$\gamma > 1$では安定な固定点となる。したがって、この系は固定点$(2n\pi, 0)$において、$\gamma=1$で超臨界ピッチフォーク分岐を起こすことがわかる。
投稿者:goodbook
投稿日時:2021-04-01 04:53:44
|
|
|
P.312の問題番号「8.1.9」
に対する解答
系$\ddot{x}+b \dot{x} -kx+x^3=0$
解)$\dot{x}=y$とすると、系は
\[ \dot{x}=y, \ \ \dot{y} = -b y + k x -x^3 \]と表すことができる。この系は
$k \leq 0$のとき、1つの固定点$(0,0)$をもち、$k>0$のとき、3つの固定点$(0,0), \ \ (\pm \sqrt{k},0)$をもつ。
各固定点でのヤコビ行列をもとめると、次のようになる。
\[ (0, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ k & -b \end{pmatrix}, \\
\tau=-b, \ \ \Delta = -k, \ \ \tau^2 - 4 \Delta = b^2+4k \]となり、$k>0$ではサドル、$k<0, \ \ b>0$では安定な固定点、$k<0, \ \ b<0$では不安定な固定点となる。
\[ (\pm \sqrt{k}, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ -2k & -b \end{pmatrix}, \\
\tau=-b, \ \ \Delta = 2k, \ \ \tau^2 - 4 \Delta = b^2-8k \]となり、$k>0, \ \ b>0$では安定な固定点、$k>0, \ \ b<0$では不安定な固定点となる。
したがって、この系は$b>0$のとき、固定点$(0,0)$において$k=0$で超臨界ピッチフォーク分岐を起こし、$b<0$のとき、固定点$(0,0)$において$k=0$で亜臨界ピッチフォーク分岐を起こすことがわかる。
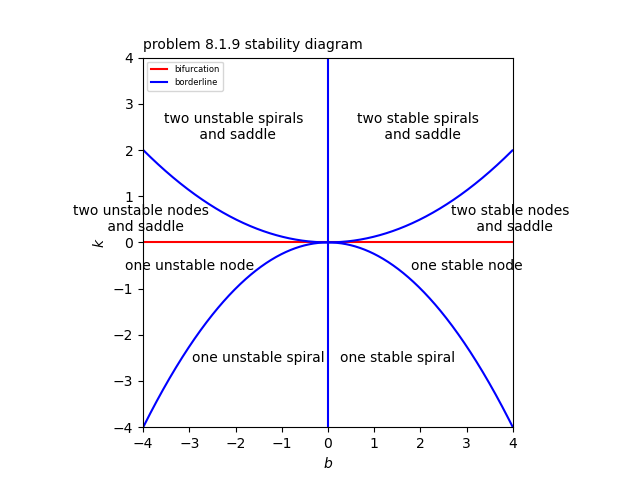
また、$(b,k)$平面において、$k<0$の領域では固定点$(0,0)$に対して$\tau^2 - 4 \Delta = b^2+4k$であるので、$k>-b^2/4$では、$b>0$のとき安定ノード、$b<0$のとき不安定ノードとなり、$k<-b^2/4$では、$b>0$のとき安定スパイラル、$b<0$のとき不安定スパイラルとなる。
一方、$k>0$の領域では2つの固定点$(\pm \sqrt{k},0)$に対して$\tau^2 - 4 \Delta = b^2-8k$であるので、$k<b^2/8$では、$b>0$のとき安定ノード、$b<0$のとき不安定ノードとなり、$k>b^2/8$では、$b>0$のとき安定スパイラル、$b<0$のとき不安定スパイラルとなる。
結果として、安定性ダイアグラムは添付図のようになる。
投稿者:goodbook
投稿日時:2021-04-02 05:10:27
|
|
|
P.312の問題番号「8.1.10」
に対する解答
\[ \dot{S} = r_S S \left( 1 - \frac{S}{K_S} \frac{K_E}{E} \right), \ \ \dot{E} = r_E E \left( 1 - \frac{E}{K_E} \right) - P \frac{B}{S} \](a) $-PB/S$は幼虫の個体数がエネルギー貯蔵$E$に与える影響を表し、幼虫が増えると、エネルギー貯蔵が減ることを示している。この幼虫の個体数の影響を無視できる場合、木の平均サイズ$S$とエネルギー貯蔵$E$はロジスティック的に増加することがわかる。ただし、木の平均サイズ$S$の環境収容力は$K_S E/K_E$でエネルギー貯蔵$E$に比例している。
(b) $x=S/K_S, \ \ y = E/K_E, \ \ t'=r_E t, \ \ r = r_S/r_E, \ \ b=PB/K_S K_E r_E$とおくと、方程式は
\[ x' = r x \left( 1 - \frac{x}{y} \right), \ \ y' = y(1-y) - \frac{b}{x} \]となる。ただし、プライムは$t'$での微分を表す。
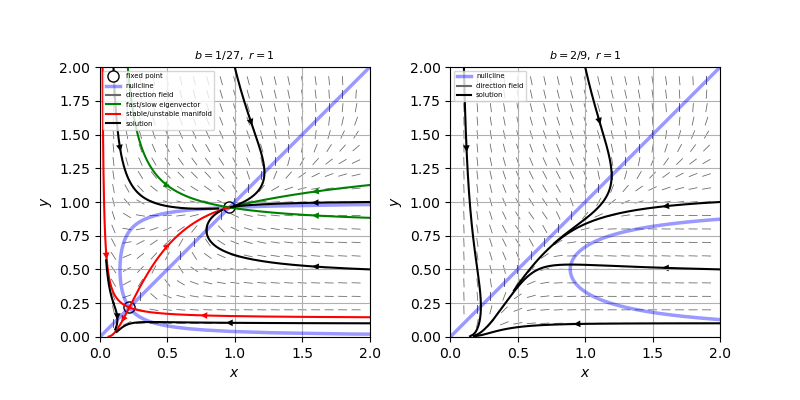
(c) ヌルクラインは添付図の青いラインとなる。
この系は$b > 4/27$のとき固定点を持たず、$b<4/27$のとき2つの固定点$(a_1, a_1), \ \ (a_2, a_2)$をもつ。ここで、
\[ a_1 = \frac{1}{3} + \frac{2}{3} \cos \frac{\alpha}{3}, \ \ a_2 = \frac{1}{3} + \frac{2}{3} \cos \left( \frac{\alpha}{3} - \frac{2}{3} \pi \right), \\
\cos \alpha = 1 - \frac{27}{2} b, \ \ \sin \alpha = \sqrt{ 27b - \frac{27^2}{4} b^2 } \]となる。各固定点でのヤコビ行列を求めると、次のようになる。
\[ (a_1, a_1) \ : \ J = \begin{pmatrix} -r & r \\ 1-a_1 & 1-2a_1 \end{pmatrix}, \ \
\tau=-r + 1 - 2a_1, \ \ \Delta = r( 3a_1 -2 ) \]となり、$2/3 < a_1 <1$を考慮すると$-r-1 < \tau < -r -1/3, \ \ 0 < \Delta < r$となるので、$(a_1,a_1)$は安定な固定点となる。一方、
\[ (a_2, a_2) \ : \ J = \begin{pmatrix} -r & r \\ 1-a_2 & 1-2a_2 \end{pmatrix}, \ \
\tau=-r + 1 - 2a_2, \ \ \Delta = r( 3a_2 -2 ) \]となり、$0 < a_2 <2/3$を考慮すると$-2r < \Delta < 0$となるので、$(a_2,a_2)$はサドルとなる。
したがって、$b=4/27$において、サドルノード分岐を起こすことがわかる。
(d) 相図は添付図のようになる。
投稿者:goodbook
投稿日時:2021-04-07 08:29:40
|
|
|
P.313の問題番号「8.1.11」
に対する解答
系$\dot{u}=a(1-u) - uv^2, \ \ \dot{v} = uv^2 - (a+k) v, \ \ a, \ k >0$
解)この系は$0<a<\frac{1}{4}, \ \ 0<k<-a+\frac{1}{2} \sqrt{a}$の領域で2つの固定点
\[ A_+ \left( \frac{a+\sqrt{a^2 - 4a(a+k)^2}}{2a}, \frac{a+\sqrt{a^2 - 4a(a+k)^2}}{2(a+k)} \right), \\
A_- \left( \frac{a-\sqrt{a^2 - 4a(a+k)^2}}{2a}, \frac{a-\sqrt{a^2 - 4a(a+k)^2}}{2(a+k)} \right) \]をもち、$0<a<\frac{1}{4}, \ \ k=-a+\frac{1}{2} \sqrt{a}$上で1つの固定点$(\frac{1}{2}, \sqrt{a})$をもち、それ以外の領域では固定点を持たない。各固定点を分類すると、
\[ A_+ \ : \ J = \begin{pmatrix} -\frac{2a^2}{a+\sqrt{a^2-4a(a+k)^2}} & -2(a+k) \\ a\frac{a-\sqrt{a^2-4a(a+k)^2}}{a+\sqrt{a^2-4a(a+k)^2}} & a+k \end{pmatrix}, \\ \tau=\frac{a(k-a)+(a+k)\sqrt{a^2-4a(a+k)^2}}{a+\sqrt{a^2-4a(a+k)^2}}, \\ \Delta = -\frac{2a(a+k)\sqrt{a^2-4a(a+k)^2}}{a+\sqrt{a^2-4a(a+k)^2}} <0 \]となるので、サドルとなる。一方、
\[ A_- \ : \ J = \begin{pmatrix} -\frac{2a^2}{a-\sqrt{a^2-4a(a+k)^2}} & -2(a+k) \\ a\frac{a+\sqrt{a^2-4a(a+k)^2}}{a-\sqrt{a^2-4a(a+k)^2}} & a+k \end{pmatrix}, \\ \tau=\frac{a(k-a)-(a+k)\sqrt{a^2-4a(a+k)^2}}{a-\sqrt{a^2-4a(a+k)^2}}, \\ \Delta = \frac{2a(a+k)\sqrt{a^2-4a(a+k)^2}}{a-\sqrt{a^2-4a(a+k)^2}} >0 \]となるので、\[ a> \frac{\sqrt{k}-2k-\sqrt{k-4k\sqrt{k}}}{4} \]のとき、安定な固定点、
\[ a< \frac{\sqrt{k}-2k-\sqrt{k-4k\sqrt{k}}}{4} \]のとき、不安定な固定点となる。
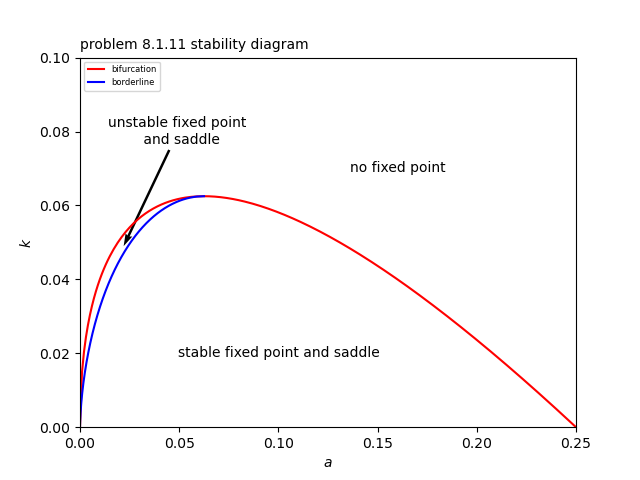
したがって、この系は$k=-a+\frac{1}{2} \sqrt{a}$でサドルノード分岐が起こることがわかる。
また、この系の安定性ダイアグラムは添付図のようになる。
投稿者:goodbook
投稿日時:2021-04-09 05:08:33
|
|
|
P.313の問題番号「8.1.12」
に対する解答
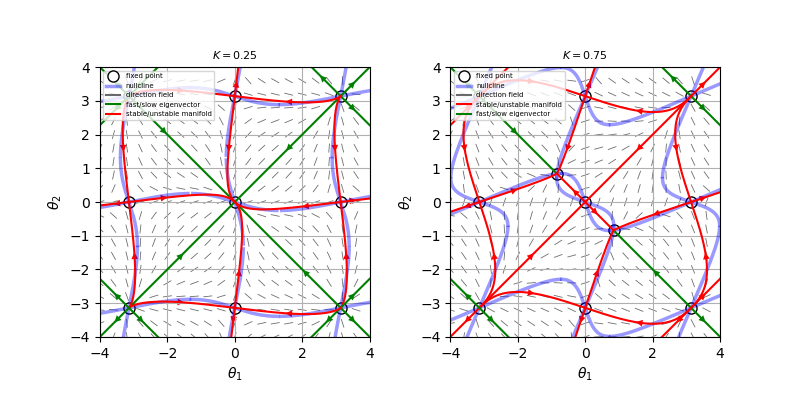
系$\dot{\theta}_1 = K \sin (\theta_1 - \theta_2) - \sin \theta_1, \ \ \dot{\theta}_2 = K \sin (\theta_2 - \theta_1) - \sin \theta_2$
(a) この系は$(m \pi, n \pi)$と、$K>\frac{1}{2}$のとき、$(2m \pi \pm \alpha, 2n\pi \mp \alpha)$に固定点をもつ。ここで、$m, \ n$は任意の整数、$\alpha$は$\cos \alpha =1/2K, \ \ \sin \alpha = \sqrt{1-4K^2}/2K$を満たす。以下、固定点ごとに分類。
\[ (2m\pi,2n\pi) \ : \ J = \begin{pmatrix} K-1 & -K \\ -K & K-1 \end{pmatrix}, \ \ \tau=2(K-1), \ \ \Delta=1-2K, \ \ \tau^2-4 \Delta=4K^2 \]となるので、$0<K<1/2$で安定ノード、$K>1/2$でサドルとなる。
\[ ((2m+1)\pi,2n\pi) \ : \ J = \begin{pmatrix} -K+1 & K \\ K & -K-1 \end{pmatrix}, \ \ \tau=-2K, \ \ \Delta=-1 \]となるので、サドルとなる。
\[ (2m\pi,(2n+1)\pi) \ : \ J = \begin{pmatrix} -K-1 & K \\ K & -K+1 \end{pmatrix}, \ \ \tau=-2K, \ \ \Delta=-1 \]となるので、サドルとなる。
\[ ((2m+1)\pi,(2n+1)\pi) \ : \ J = \begin{pmatrix} K+1 & -K \\ -K & K+1 \end{pmatrix}, \\ \tau=2(K+1), \ \ \Delta=1+2K, \ \ \tau^2-4 \Delta=4K^2 \]となるので、不安定ノードとなる。
\[ (2m\pi \pm \alpha,2n\pi \mp \alpha) \ : \ J = \begin{pmatrix} -K & K-\frac{1}{2K} \\ K-\frac{1}{2K} & -K \end{pmatrix}, \\ \tau=-2K, \ \ \Delta=1-\frac{1}{4K^2}, \ \ \tau^2-4 \Delta=(2K-\frac{1}{K})^2 \]となるので、安定ノードとなる。
(b) (a)の結果より、$K=\frac{1}{2}$のとき$(2m\pi,2n\pi)$で超臨界ピッチフォーク分岐を起こすことがわかる。
(c) この系のポテンシャルは
\[ V(\theta_1,\theta_2) = -K \cos(\theta_1-\theta_2) + \cos \theta_1 + \cos \theta_2 \]と表すことできるので、この系は勾配系であることがわかる。
(d) (c)の結果と定理7.2.1により、周期軌道はもたないことがわかる。
(e) 相図は添付図参照。
投稿者:goodbook
投稿日時:2021-04-11 09:02:25
|
|
|
P.314の問題番号「8.1.13」
に対する解答
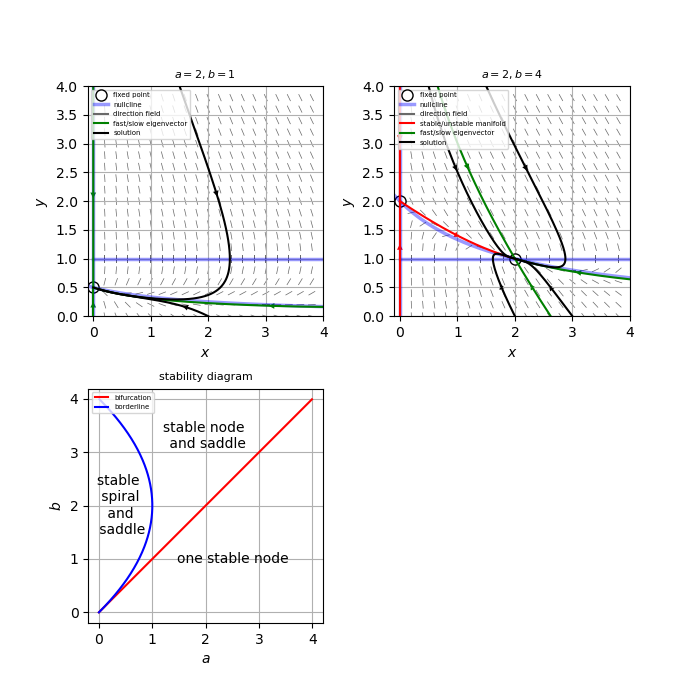
系$\dot{n}=GnN-kn, \ \ \dot{N}=-GnN-fN+p$
(a) $x=Gn/k, \ \ y=GN//k, \ \ t'=kt, \ \ a=f/k, \ \ b=Gp/k^2$とおくと、系は
\[ x'=xy-x, \ \ y'=-xy-ay+b \]と表すことができる。ここで、プライムは$t'$での微分を表す。
(b) この系は$(0,b/a), \ \ (b-a,1)$に固定点をもつ。以下、固定点ごとに分類。
\[ (0,\frac{b}{a}) \ : \ J = \begin{pmatrix} \frac{b}{a}-1 & 0 \\ -\frac{b}{a} & -a \end{pmatrix}, \ \ \tau=\frac{b}{a}-1-a, \ \ \Delta=a-b, \ \ \tau^2-4 \Delta=(\frac{b}{a}-1+a)^2 \]となるので、$b<a$で安定ノード、$b>a$でサドルとなる。
\[ (b-a,1) \ : \ J = \begin{pmatrix} 0 & b-a \\ -1 & -b \end{pmatrix}, \ \ \tau=-b, \ \ \Delta=b-a, \ \ \tau^2-4 \Delta=b^2-4b+4a \]となるので、$b>a$で$a<b-\frac{b^2}{4}$のとき安定スパイラル、$a>b-\frac{b^2}{4}$のとき安定ノードとなる。
(c) 相図は添付図。
(d) この系では$b=a$でトランスクリティカル分岐が起こる。
投稿者:goodbook
投稿日時:2021-04-11 14:14:09
|
|





