|
P.314の問題番号「8.2.1」
に対する解答
バイアスのかかったファン・デル・ポール振動子$\ddot{x} + \mu (x^2-1) \dot{x} + x = a$
解)$\dot{x}=y$とおくと、方程式は
\[ \dot{x}=y, \ \ \dot{y} = -x - \mu (x^2-1)y+a \]と表すことができる。この系の固定点は$(a,0)$となる。ヤコビ行列は
\[ J = \begin{pmatrix} 0 & 1 \\ -1 & -\mu(a^2-1) \end{pmatrix}, \ \ \tau=-\mu (a^2-1), \ \ \Delta =1>0, \ \ \tau^2 - 4 \Delta = \mu^2(a^2-1)^2-4 \]となり、固有値は
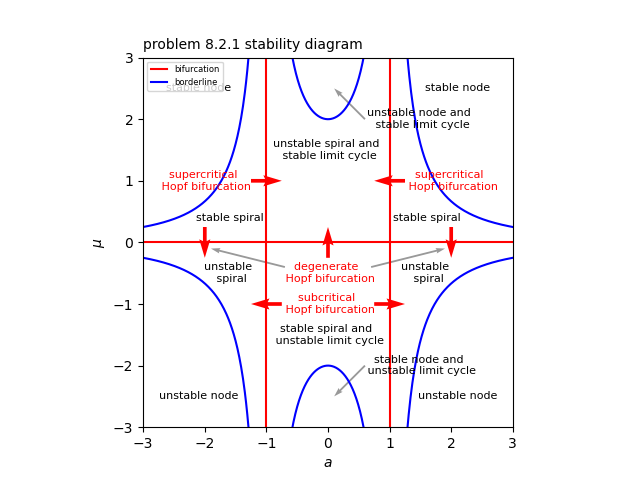
\[ \lambda = \frac{-\mu(a^2-1) \pm \sqrt{\mu^2 (a^2-1)^2-4} }{2} \]となる。したがって、$(a,\mu)$平面において、安定性ダイアグラムを描くと添付図のようになり、赤い線がホップ分岐が起こる曲線となる。
i) $a,\mu$が$|a|>1, \ \ \mu>0$の領域から$|a|<1, \ \ \mu>0$の領域に移動するとき、超臨界ホップ分岐が起こる。
ii) $a,\mu$が$|a|<1, \ \ \mu<0$の領域から$|a|>1, \ \ \mu<0$の領域に移動するとき、亜臨界ホップ分岐が起こる。
iii) $a,\mu$が$|a|>1, \ \ \mu>0$の領域から$|a|>1, \ \ \mu<0$の領域に移動するとき、退化したホップ分岐が起こる。
iv) $a,\mu$が$|a|<1, \ \ \mu<0$の領域から$|a|<1, \ \ \mu>0$の領域に移動するとき、退化したホップ分岐が起こる。
投稿者:goodbook
投稿日時:2021-04-13 06:39:26
|
|
|
P.314の問題番号「8.2.2」
に対する解答
系$\dot{x}=-y+ \mu x + x y^2, \ \ \dot{y}=x+ \mu y - x^2$
解)この系の原点における線形化方程式を計算すると、
\[ \begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix} = \begin{pmatrix} \mu & -1 \\ 1 & \mu \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \]となる。したがって、ヤコビ行列は
\[ J = \begin{pmatrix} \mu & -1 \\ 1 & \mu \end{pmatrix}, \ \ \tau=2 \mu, \ \ \Delta = \mu^2+1>0, \ \ \tau^2 - 4 \Delta = -4 \]となり、その固有値は
\[ \lambda = \mu \pm i \]となる。これは$\mu=0$のとき、純虚数の固有値を持つことを示す。
投稿者:goodbook
投稿日時:2021-04-17 08:36:21
|
|
|
P.314の問題番号「8.2.3」
に対する解答
系$\dot{x}=-y+ \mu x + x y^2, \ \ \dot{y}=x+ \mu y - x^2$
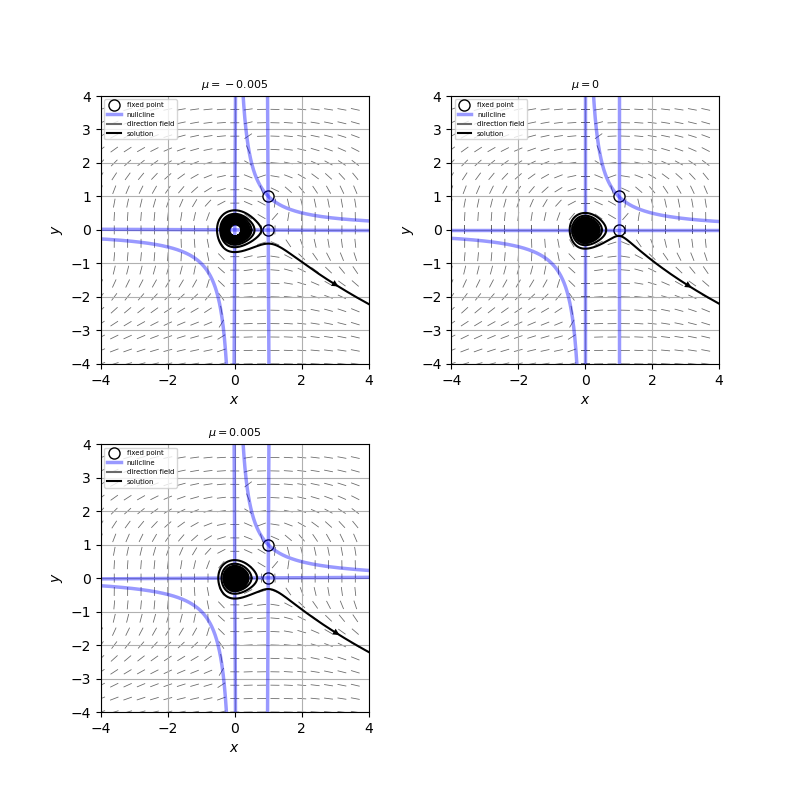
この系の相図をコンピュータ上でプロットすると、添付図のようになる。
$\mu<0$のとき、原点付近に不安定なリミットサイクルが見つかる。$\mu$が次第に大きくなっていくと、不安定なリミットサイクルは原点周りに縮まっていき、$\mu=0$で亜臨界ホップ分岐が起こる。
投稿者:goodbook
投稿日時:2021-04-17 08:38:09
|
|
|
P.314の問題番号「8.2.4」
に対する解答
系$\dot{x}=-y+ \mu x + x y^2, \ \ \dot{y}=x+ \mu y - x^2$
(a) この系を極座標で表すと、
\[ \dot{r} = \mu r - \frac{r^2}{4} (\sin \theta + \sin 3 \theta) + \frac{r^3}{8} (1- \cos 4 \theta) \\
\dot{\theta} = 1 - \frac{r}{4} (3 \cos \theta + \cos 3 \theta) - \frac{r^2}{8} (2 \sin 2 \theta - \sin 4 \theta) \]となる。
(b) (a)の結果から、$r \ll 1$で振動的な項を無視すると、
\[ \dot{\theta} \approx 1, \ \ \dot{r} \approx \mu r + \frac{r^3}{8} + \cdots \]が得られる。
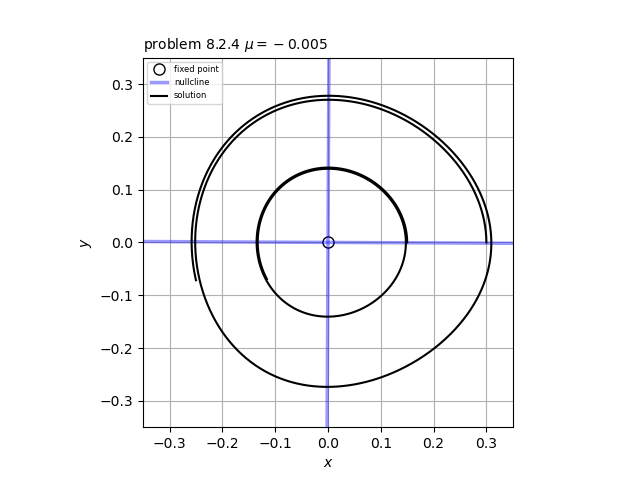
(c) $\mu=-0.005$のときの原点付近の軌道を描くと添付図のようになる。点$(0.3,0)$からはじまる軌道は原点から遠ざかる方向に向かっていることがわかる。一方、点$(0.15,0)$からはじまる軌道は原点に近づく方向に向かっていることがわかる。したがって、$\mu=-0.005<0$で半径$r \approx \sqrt{-8 \mu} = 0.2$の不安定リミットサイクルが存在することが示唆される。
投稿者:goodbook
投稿日時:2021-04-17 08:40:52
|
|
|
P.314の問題番号「8.2.5」
に対する解答
系$\dot{x} = y+ \mu x, \ \ \dot{y} = -x + \mu y -x^2 y$
この系の原点でのヤコビ行列は
\[ J = \begin{pmatrix} \mu & 1 \\ -1 & \mu \end{pmatrix}, \ \ \tau=2 \mu, \ \ \Delta = \mu^2+1>0, \ \ \tau^2 - 4 \Delta = -4 \]となり、その固有値は
\[ \lambda = \mu \pm i \]となるので、この系は$\mu=0$のとき原点でホップ分岐を起こすことがわかる。
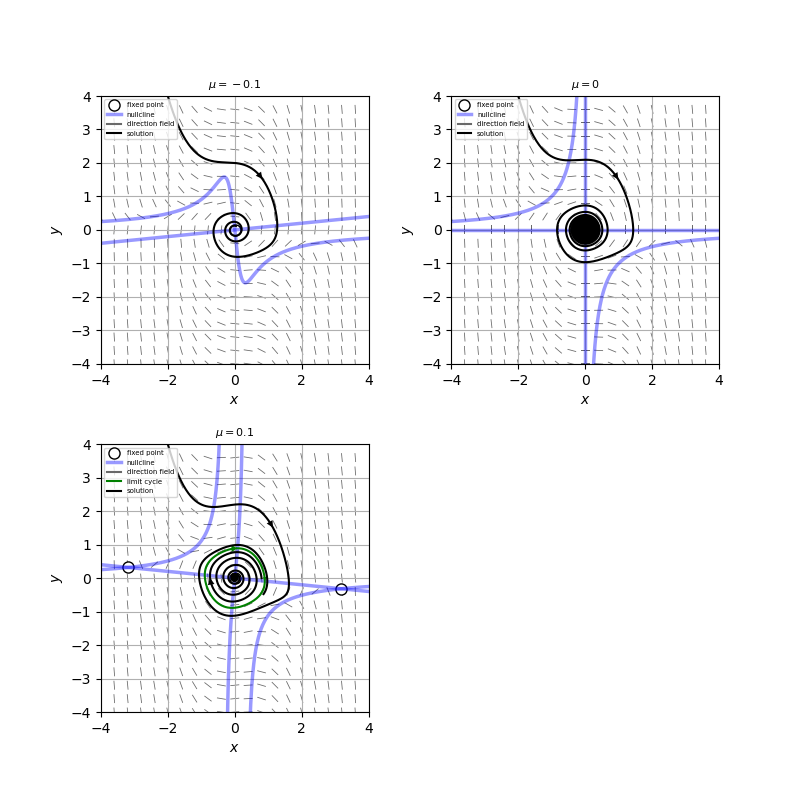
この系の相図を描くと、添付図のようになる。
$\mu<0$のとき、原点は安定スパイラルで、$\mu>0$のとき原点は不安定スパイラルとなり、また原点周りに安定なリミットサイクルが現れるので、この系は超臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-18 08:35:29
|
|
|
P.315の問題番号「8.2.6」
に対する解答
系$\dot{x} = \mu x + y -x^3, \ \ \dot{y} = -x + \mu y + 2 y^3$
この系の原点でのヤコビ行列は
\[ J = \begin{pmatrix} \mu & 1 \\ -1 & \mu \end{pmatrix}, \ \ \tau=2 \mu, \ \ \Delta = \mu^2+1>0, \ \ \tau^2 - 4 \Delta = -4 \]となり、その固有値は
\[ \lambda = \mu \pm i \]となるので、この系は$\mu=0$のとき原点でホップ分岐を起こすことがわかる。
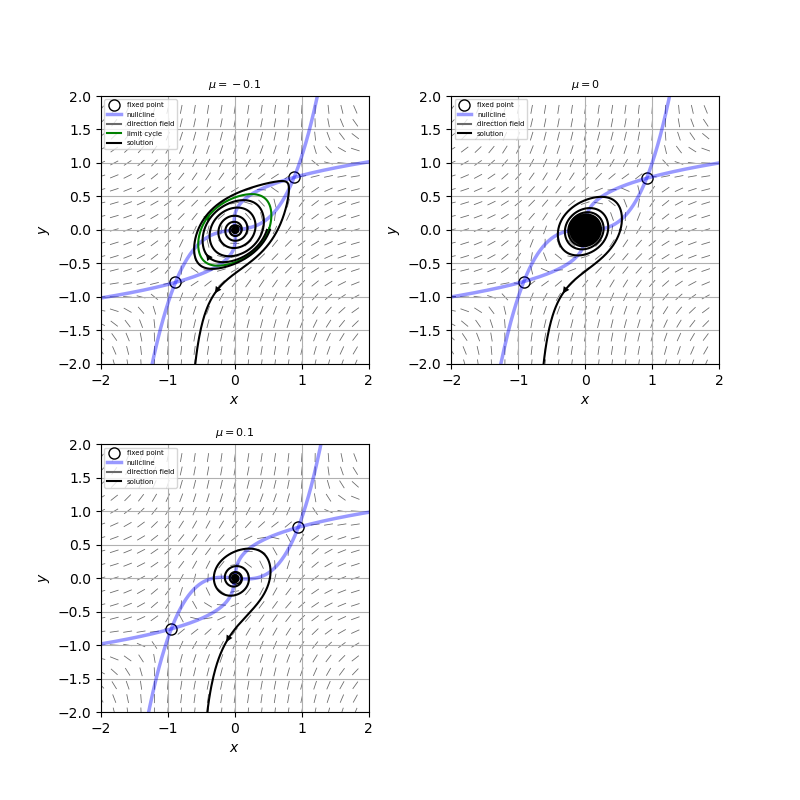
この系の相図を描くと、添付図のようになる。
$\mu<0$のとき、原点は安定スパイラルで、また原点周りに不安定なリミットサイクルが現れ、$\mu>0$のとき原点は不安定スパイラルとなり、不安定なリミットサイクルは消えるので、この系は亜臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-18 14:58:34
|
|
|
P.315の問題番号「8.2.7」
に対する解答
系$\dot{x} = \mu x + y -x^2, \ \ \dot{y} = -x + \mu y + 2 x^2$
この系の原点でのヤコビ行列は
\[ J = \begin{pmatrix} \mu & 1 \\ -1 & \mu \end{pmatrix}, \ \ \tau=2 \mu, \ \ \Delta = \mu^2+1>0, \ \ \tau^2 - 4 \Delta = -4 \]となり、その固有値は
\[ \lambda = \mu \pm i \]となるので、この系は$\mu=0$のとき原点でホップ分岐を起こすことがわかる。
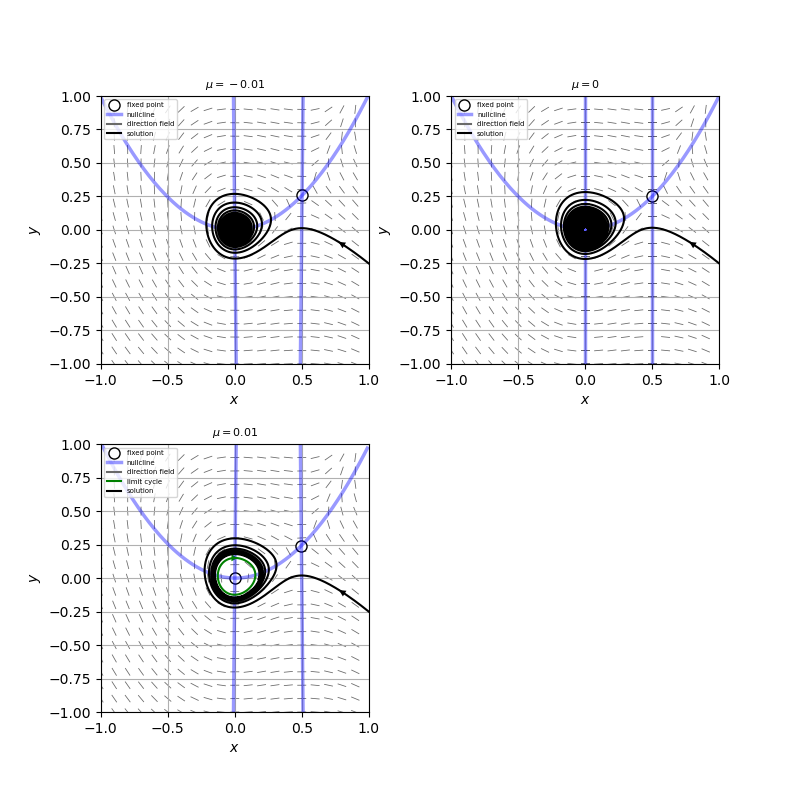
この系の相図を描くと、添付図のようになる。
$\mu<0$のとき、原点は安定スパイラルで、$\mu>0$のとき原点は不安定スパイラルとなり、また原点周りに安定なリミットサイクルが現れるので、この系は超臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-18 16:12:33
|
|
|
P.315の問題番号「8.2.8」
に対する解答
系$\dot{x}=x[x(1-x)-y], \ \ \dot{y}=y(x-a)$
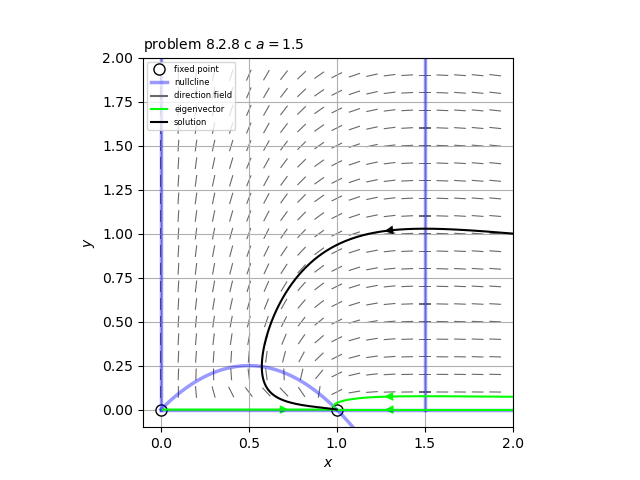
(a) ヌルクラインは添付図の青いライン。
(b) 固定点は$(0,0), \ \ (1,0), \ \ (a, a-a^2)$の3点。以下、各固定点ごとに分類。
\[ (0,0) \ : \ J = \begin{pmatrix} 0 & 0 \\ 0 & -a \end{pmatrix}, \ \ \tau=-a, \ \ \Delta = 0, \ \ \tau^2 - 4 \Delta = a^2 \geq 0 \]となるので、孤立していない固定点と予想される。
\[ (1,0) \ : \ J = \begin{pmatrix} -1 & -1 \\ 0 & 1-a \end{pmatrix}, \ \ \tau=-a, \ \ \Delta = a-1, \ \ \tau^2 - 4 \Delta = (a-2)^2 \geq 0 \]となるので、$0 \leq a<1$のときサドル、$a>1$のとき安定ノードとなる。
\[ (a,a-a^2) \ : \ J = \begin{pmatrix} a-2a^2 & -a \\ a-a^2 & 0 \end{pmatrix}, \ \ \tau=a-2a^2, \ \ \Delta = a^2(1-a), \ \ \tau^2 - 4 \Delta = a^2(4a^2-3) \]となるので、$0 \leq a < \frac{1}{2}$のとき不安定スパイラル、$\frac{1}{2}<a<1$のとき安定な固定点となり、$a>1$のときサドルとなる。また、固有値は
\[ \lambda = \frac{a(1-2a) \pm a \sqrt{4a^2-3}}{2} \]となる。
(c) $a>1$における相図は添付図のようになる。ほぼすべての軌道は安定固定点$(1,0)$に向かう。つまり、捕食者は絶滅する。
投稿者:goodbook
投稿日時:2021-04-21 05:20:16
|
|
|
P.315の問題番号「8.2.9」
に対する解答
\[ \dot{x}=x(b-x-\frac{y}{1+x}), \ \ \dot{y}=y(\frac{x}{1+x}-ay) \] (a) この系のヌルクラインは$\dot{x}=0, \ \dot{y}=0$より、$x=0, \ \ y=(1+x)(b-x), \ \ y=0, \ \ y=\frac{x}{a(1+x)}$となる。これらを描くと、添付図の青いラインのようになる。
(b) すべての$a,b>0$において、ヌルクライン$y=(1+x)(b-x)$は点$(b,0)$と点$(0,b)$を通り、一方、$y=\frac{x}{a(1+x)}$は原点を通り、$y=1/a$に$x$が正の向きに漸近する関数になっているので、この2つのヌルクラインは必ず第1象限で交わる。つまり、正の固定点$x^*>0, \ \ y^*>0$が存在することがわかる。
(c) この系の固定点は$(0,0), \ \ (b,0), \ \ (x^*,y^*)$の3点。このうち、$(0,0)$は孤立していない固定点と予想され、$(b,0)$はサドルとなる。
\[ (x^*,y^*) \ : \ J = \frac{1}{1+x^*} \begin{pmatrix} x^*((b-1)-2x^*) & -x^* \\ b-x^* & -x^* \end{pmatrix}, \\
\tau=\frac{x^*((b-2)-2x^*)}{1+x^*}, \ \ \Delta = \frac{x^*(b-bx^*+2x^{*2})}{(1+x^*)^2} \]となる。ここで、$\tau=0$より$2x^*=b-2$が得られ、このとき、
\[ \Delta=\frac{4(b-2)}{b^2}, \ \ \tau^2-4\Delta=-\frac{16(b-2)}{b^2} \]となるので、$b>2$のとき、ホップ分岐が起こることがわかる。また、このとき、
\[ a_c=\frac{x^*}{(b-x^*)(1+x^*)^2}=\frac{4(b-2)}{b^2(b+2)} \]となる。
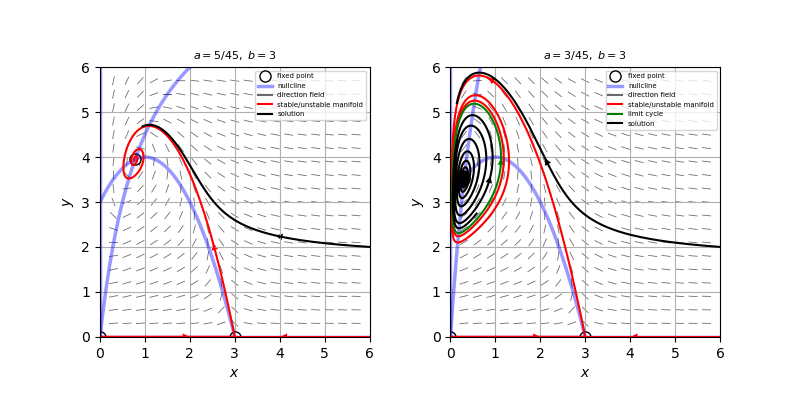
(d) まず、$a$と$x^*$の関係を考える。$b$の値が固定されているとすると、ヌルクライン$y=(1+x)(b-x)$も固定される。このとき、$a$を大きくしていくと、ヌルクライン$y=\frac{x}{a(1+x)}$は$y=0$に近づいていくので、$x^*$は大きくなりながら、$b$に近づいていくことがわかる。したがって、$a>a_c$のとき$\tau<0$、$a<a_c$のとき$\tau>0$となる。これを踏まえて、$b=3, \ \ a_c=4/45$のときの相図を描くと添付図のようになり、この系は$a>a_c$のとき$(x^*,y^*)$は安定スパイラルとなり、$a<a_c$のとき$(x^*,y^*)$は不安定スパイラルで、その周りに安定なリミットサイクルを持つので、超臨界ホップ分岐を起こすことわかる。
投稿者:goodbook
投稿日時:2021-04-23 05:31:43
|
|
|
P.315の問題番号「8.2.10」
に対する解答
\[ \dot{x}=B-x-\frac{xy}{1+qx^2}, \ \ \dot{y}=A-\frac{xy}{1+qx^2} \] 解)この系の固定点は
\[ \left( B-A, \frac{A(1+q(B-A)^2)}{B-A} \right) \]となる。この固定点でのヤコビ行列は
\[ J = \begin{pmatrix} -1+\frac{A(q(B-A)^2-1)}{(B-A)(1+q(B-A)^2)} & -\frac{B-A}{1+q(B-A)^2} \\ \frac{A(q(B-A)^2-1)}{(B-A)(1+q(B-A)^2)} & -\frac{B-A}{1+q(B-A)^2} \end{pmatrix}, \\
\tau=\frac{q(2A-B)(B-A)^2-B-(B-A)^2}{(B-A)(1+q(B-A)^2)}, \ \ \Delta = \frac{B-A}{1+q(B-A)^2} \]となる。ホップ分岐が起こる条件は$\tau=0, \ \ \Delta>0$であることから、
\[ q = \frac{B+(B-A)^2}{(2A-B)(B-A)^2}, \ \ B>A \]のとき、ホップ分岐が起こることがわかる。また、$q>0$であるので、$A,B$に対する条件は、
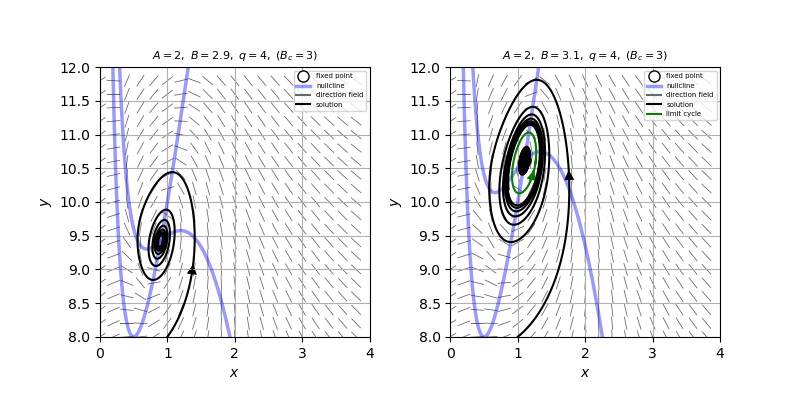
\[ A<B<2A \]となる。これらの式を満たす$A,B,q$をそれぞれ$A_c, B_c, q_c$とおく。添付図に$A_c=2, \ \ B_c=3, \ \ q_c=4$としたとき、$B<B_c$と$B>B_c$の場合の相図を示す。$B<B_c$のとき、$\tau<0$となり、固定点は安定スパイラルになる。一方、$B>B_c$のとき$\tau>0$となり、固定点は不安定スパイラルとなり、その周りに安定なリミットサイクルが現れる。したがって、この系は超臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-25 07:56:32
|
|





