|
P.316の問題番号「8.2.11」
に対する解答
減衰を受けるダフィン振動子$\ddot{x}+\mu \dot{x} + x-x^3=0$
(a) $\dot{x}=y$とおくと、方程式は
\[ \dot{x}=y, \ \ \dot{y}=-\mu y -x+x^3 \]と書くことができる。この系の固定点は$(0,0), \ \ (\pm 1, 0)$。以下、各固定点について分類。
\[ (\pm 1, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ 1 & -\mu \end{pmatrix}, \ \ \tau=-\mu, \ \ \Delta = -1<0 \]となるので、サドルとなる。
\[ (0, 0) \ : \ J = \begin{pmatrix} 0 & 1 \\ -1 & -\mu \end{pmatrix}, \ \ \tau=-\mu, \ \ \Delta = 1>0 \]となるので、$\mu>0$のとき、安定スパイラルとなり、$\mu$が$0$未満まで減少すると、不安定スパイラルに変わることがわかる。
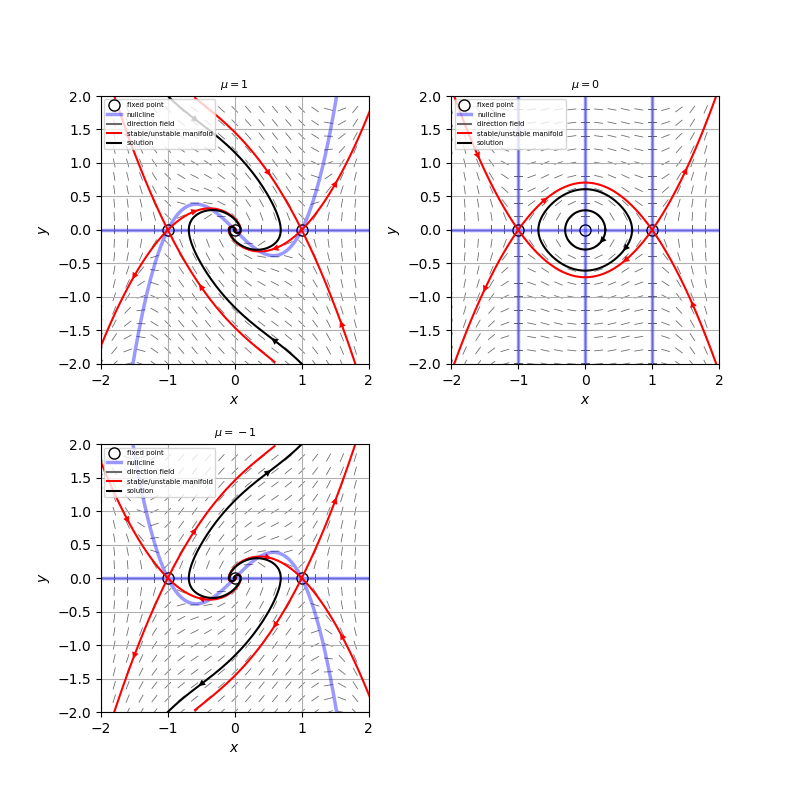
(b) この系の相図を添付図に示す。相図より、$\mu=0$において、原点を囲む閉軌道の連続的な帯をもっているので、$\mu=0$における分岐がホップ分岐の退化版であることがわかる。
投稿者:goodbook
投稿日時:2021-04-25 17:30:18
|
|
|
P.316の問題番号「8.2.12」
に対する解答
(a) 系$\dot{x}=-y+xy^2, \ \ \dot{y}=x-x^2$
解)この系では$\omega=1, \ \ f(x,y)=xy^2, \ \ g(x,y)=-x^2$となる。原点では
\[ f_x = y^2, \ \ f_y=2xy, \ \ g_x=-2x, \ \ g_y=0, \\
f_{xx}=0, \ \ f_{xy}=2y=0, \ \ f_{yy}=2x=0, \ \ g_{xx}=-2, \ \ g_{xy}=0, \ \ g_{yy}=0, \\
f_{xxx}=0, \ \ f_{xyy}=2, \ \ g_{xxy}=0, \ \ g_{yyy}=0 \]となるので、$a=1/8$が得られる。
(b) 系$\dot{x}=-y+ \mu x +xy^2, \ \ \dot{y}=x+ \mu y-x^2$は演習問題8.2.2より原点でホップ分岐を起こしている。また、(a)の結果からこの分岐は亜臨界であることがわかる。これは演習問題8.2.2-8.2.4の結果と一致する。
投稿者:goodbook
投稿日時:2021-04-26 06:25:54
|
|
|
P.316の問題番号「8.2.13」
に対する解答
系$\dot{x}=y+ \mu x, \ \ \dot{y}=-x + \mu y - x^2 y$
ホップ分岐点で系は$\dot{x}=y, \ \ \dot{y}=-x - x^2 y$となる。$\omega=-1, \ \ f(x,y)=0, \ \ g(x,y)=-x^2y$とおくと、
\[ f_x = 0, \ \ f_y=0, \ \ g_x=-2xy, \ \ g_y=-x^2, \\
f_{xx}=0, \ \ f_{xy}=0, \ \ f_{yy}=0, \ \ g_{xx}=-2y=0, \ \ g_{xy}=-2x=0, \ \ g_{yy}=0, \\
f_{xxx}=0, \ \ f_{xyy}=0, \ \ g_{xxy}=-2, \ \ g_{yyy}=0 \]となるので、$a=-1/8$が得られる。したがって、この系は超臨界ホップ分岐を起こすことがわかる。
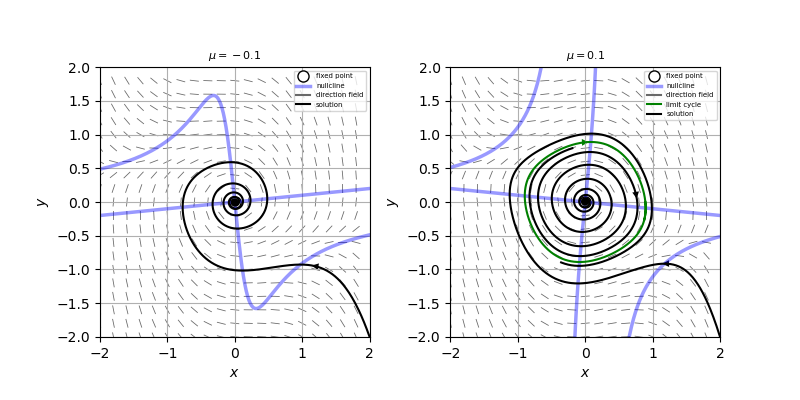
また、$\mu<0, \ \ \mu>0$での相図を描くと添付図のようになり、実際、超臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-27 06:09:39
|
|
|
P.317の問題番号「8.2.14」
に対する解答
系$\dot{x}=\mu x + y -x^3, \ \ \dot{y}=-x + \mu y + 2 y^3$
ホップ分岐点で系は$\dot{x}=y-x^3, \ \ \dot{y}=-x +2 y^3$となる。$\omega=-1, \ \ f(x,y)=-x^3, \ \ g(x,y)=2y^3$とおくと、
\[ f_x = -3x^2, \ \ f_y=0, \ \ g_x=0, \ \ g_y=6y^2, \\
f_{xx}=-6x=0, \ \ f_{xy}=0, \ \ f_{yy}=0, \ \ g_{xx}=0, \ \ g_{xy}=0, \ \ g_{yy}=12y=0, \\
f_{xxx}=-6, \ \ f_{xyy}=0, \ \ g_{xxy}=0, \ \ g_{yyy}=12 \]となるので、$a=3/8$が得られる。したがって、この系は亜臨界ホップ分岐を起こすことがわかる。
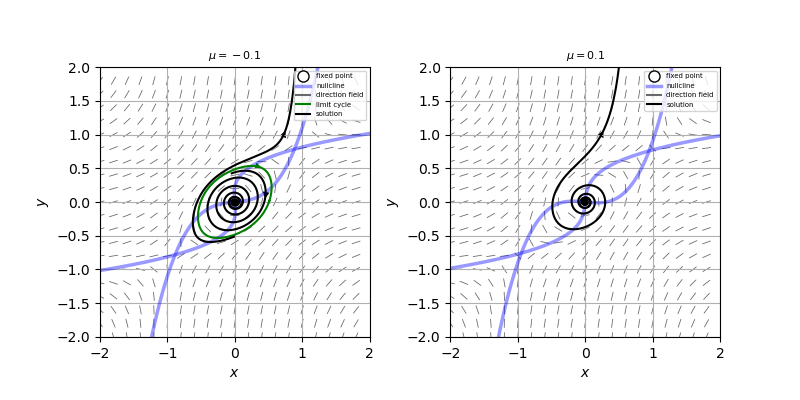
また、$\mu<0, \ \ \mu>0$での相図を描くと添付図のようになり、実際、亜臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-28 05:10:50
|
|
|
P.317の問題番号「8.2.15」
に対する解答
系$\dot{x}=\mu x +y -x^2, \ \ \dot{y}=-x + \mu y + 2 x^2$
ホップ分岐点で系は$\dot{x}=y-x^2, \ \ \dot{y}=-x + 2 x^2$となる。$\omega=-1, \ \ f(x,y)=-x^2, \ \ g(x,y)=2x^2$とおくと、
\[ f_x = -2x, \ \ f_y=0, \ \ g_x=4x, \ \ g_y=0, \\
f_{xx}=-2, \ \ f_{xy}=0, \ \ f_{yy}=0, \ \ g_{xx}=4, \ \ g_{xy}=0, \ \ g_{yy}=0, \\
f_{xxx}=0, \ \ f_{xyy}=0, \ \ g_{xxy}=0, \ \ g_{yyy}=0 \]となるので、$a=-1/2$が得られる。したがって、この系は超臨界ホップ分岐を起こすことがわかる。
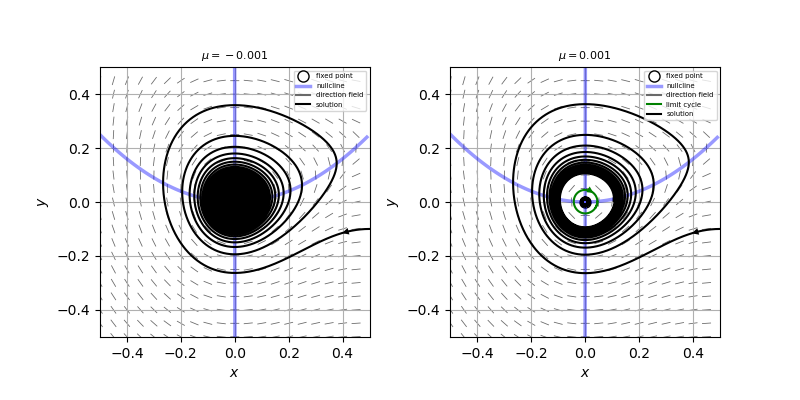
また、$\mu<0, \ \ \mu>0$での相図を描くと添付図のようになり、実際、超臨界ホップ分岐を起こしていることがわかる。
投稿者:goodbook
投稿日時:2021-04-28 06:09:00
|
|
|
P.317の問題番号「8.2.16」
に対する解答
系$\dot{x}=\mu x - y +x y^2, \ \ \dot{y}=x + \mu y + y^3$
ホップ分岐点で系は$\dot{x}=-y+x y^2, \ \ \dot{y}=x + y^3$となる。$\omega=1, \ \ f(x,y)=xy^2, \ \ g(x,y)=y^3$とおくと、
\[ f_x = y^2, \ \ f_y=2xy, \ \ g_x=0, \ \ g_y=3y^2, \\
f_{xx}=0, \ \ f_{xy}=2y=0, \ \ f_{yy}=2x=0, \ \ g_{xx}=0, \ \ g_{xy}=0, \ \ g_{yy}=6y=0, \\
f_{xxx}=0, \ \ f_{xyy}=2, \ \ g_{xxy}=0, \ \ g_{yyy}=6 \]となるので、$a=1/2$が得られる。したがって、この系は亜臨界ホップ分岐を起こすことがわかる。
投稿者:goodbook
投稿日時:2021-04-28 06:20:55
|
|
|
P.317の問題番号「8.3.1」
に対する解答
系$\dot{x}=1-(b+1)x+ax^2y, \ \ \dot{y}=bx-ax^2y$
(a) この系の固定点は$(1,b/a)$。ヤコビ行列は
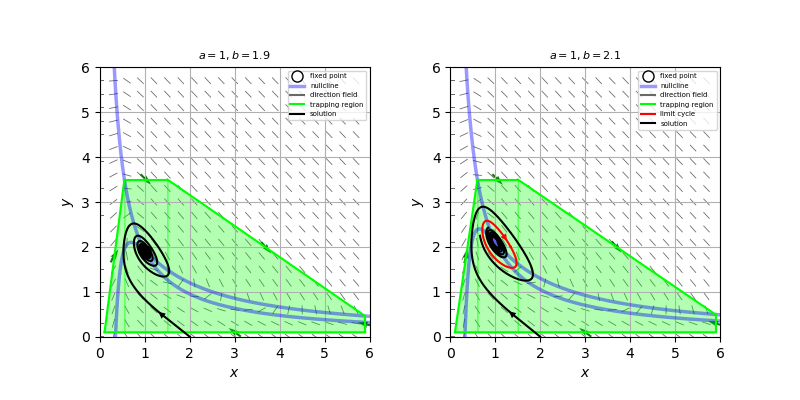
\[ J = \begin{pmatrix} b-1 & a \\ -b & -a \end{pmatrix}, \ \ \tau=b-a-1, \ \ \Delta =a \]となるので、$b<a+1$のとき安定スパイラルとなり、$b>a+1$のとき不安定スパイラルとなる。
(b) 添付図参照。ヌルクラインは青線で、トラッピング領域は例えば緑色の領域のようにとれる。
(c) $b_c=a+1$とすると、(a)の結果より$b<b_c$のとき$\tau<0, \ \ \Delta>0$であるので固有値の実部は負であり、$b$が増加し$b>b_c$となると$\tau>0, \ \ \Delta>0$となるので固有値の実部は生となる。つまり、$b=b_c$でホップ分岐を起こすことがわかる。
(d) (b)の結果から添付図のようにトラッピング領域を構成できる。したがって、$b>b_c$のとき、固定点がリペラーになることを考慮すると、ポアンカレ-ベンディクソンの定理よりリミットサイクルが存在することがわかる。
(e) 振動数は分岐点における固有値の虚部によって近似されるので、
\[ \omega \approx \sqrt{\Delta} = \sqrt{a} \]となる。したがって、リミットサイクルの周期は
\[ T \approx \frac{2\pi}{\sqrt{a}} \]で近似される。
投稿者:goodbook
投稿日時:2021-05-01 06:01:44
|
|
|
P.317の問題番号「8.3.2」
に対する解答
系$\dot{x}=a-x+x^2y, \ \ \dot{y}=b-x^2y$
(a) ヌルクライン$y=(x-a)/x^2$と$x$軸との交点$(a,0)$から始める。点$(a,0)$に接する直線をもう一つのヌルクライン$y=b/x^2$と交わる点$(x_1,y_1)$まで延ばす。次に、$x \geq a+b, \ \ y>(x-a)/x^2$の領域で$\dot{y}/\dot{x} \leq -1$となることを考慮して、点$(x_1,y_1)$から$x$軸と平行に点$(a+b,y_1)$まで線を延ばし、その後、点$(a+b,y_1)$から傾き$-1$の線を$y=(x-a)/x^2$と交わる点$(x_2,y_2)$まで延ばす。その点$(x_2,y_2)$から$x$軸に垂線を下ろすと、ここまで描いた線と$x$軸で囲まれた領域はトラッピング領域となる。添付図にトラッピング領域(緑の領域)を描く。
(b) この系の固定点は$(a+b,b/(a+b)^2)$。ヤコビ行列は
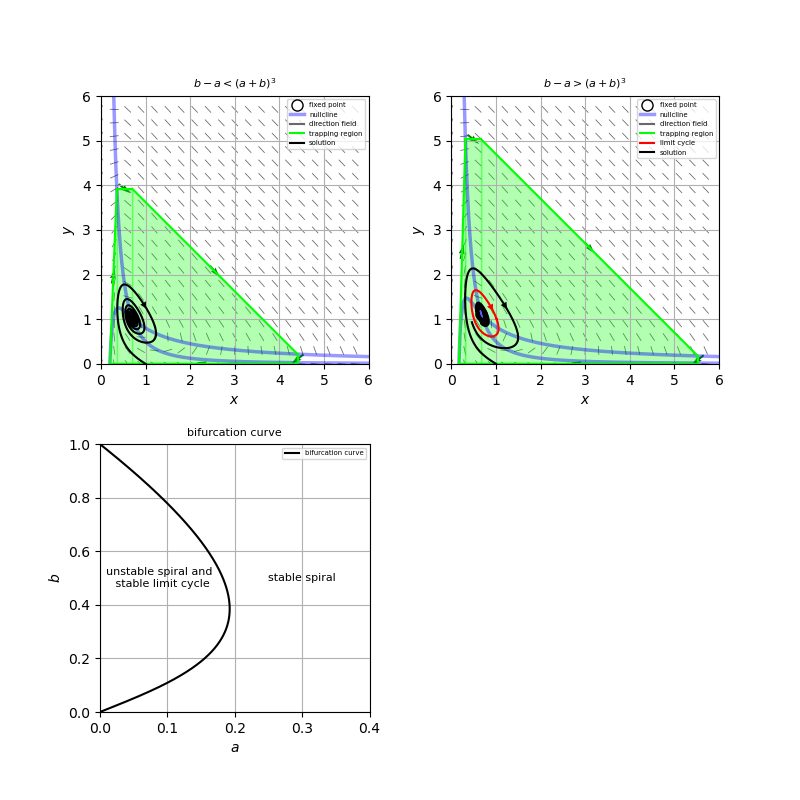
\[ J = \begin{pmatrix} -1 + \frac{2b}{a+b} & (a+b)^2 \\ -\frac{2b}{a+b} & -(a+b)^2 \end{pmatrix}, \ \ \tau=\frac{b-a-(a+b)^3}{a+b}, \ \ \Delta =(a+b)^2 \]となるので、$b-a<(a+b)^3$のとき安定スパイラルとなり、$b-a>(a+b)^3$のとき不安定スパイラルとなる。
(c) (b)の結果より$b-a<(a+b)^3$のとき$\tau<0, \ \ \Delta>0$であるので固有値の実部は負であり、$a, \ b$が変化し$b-a>(a+b)^3$となると$\tau>0, \ \ \Delta>0$となるので固有値の実部は正となる。つまり、$b-a=(a+b)^3$でホップ分岐を起こすことがわかる。
(d) この系の相図は添付図の上段2つの図のようになる。その結果、この系は超臨界ホップ分岐を起こすことがわかる。
(e) 固定点の$x$座標を$x^*=a+b$とおく。このとき、分岐の条件式から$b-a=(x^*)^3$となる。したがって、この2式から
\[ a=\frac{1}{2} x^* [1-(x^*)^2], \ \ b=\frac{1}{2} x^* [1+(x^*)^2] \]を得る。これらを使うと、分岐曲線は添付図の下図のようになる。
投稿者:goodbook
投稿日時:2021-05-01 16:23:32
|
|
|
P.318の問題番号「8.3.3」
に対する解答
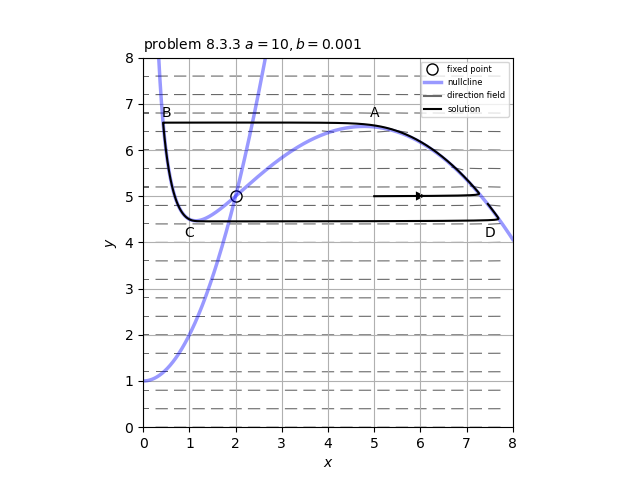
系\[ \dot{x}=a-x-\frac{4xy}{1+x^2}, \ \ \dot{y}=bx \left( 1-\frac{y}{1+x^2} \right) \] リミットサイクルを持つ場合を考える。$b \ll 1$の場合$|\dot{y}| \sim \mathcal{O}(b)$となるので、$a-x-\frac{4xy}{1+x^2} \sim \mathcal{O}(1)$の領域では、ベクトル場の流れの速度は水平方向に大きく、垂直方向には小さいため、軌道はほとんど水平方向に動く。初期条件がヌルクライン$y=(a-x)(1+x^2)/4x$より下側にある場合、$a-x-\frac{4xy}{1+x^2}>0$となるので、$\dot{x}>0$である。つまり軌道はヌルクラインに向かって横向き正の方向に動く。その後、軌道がヌルクラインにきわめて近接し、$y-(a-x)(1+x^2)/4x \sim \mathcal{O}(b)$となると、$\dot{x}$および$\dot{y}$は同程度の大きさをもち、ヌルクラインの近傍に沿ってゆっくりと$\mathcal{O}(b)$程度の速度で移動して添付図の点AまたはCの屈曲部に至り、再び横向きにジャンプする。
この系の固定点の$x$座標を$x^*$とおくと、
\[ x^* = \frac{a}{5}, \ \ \Delta = \frac{5bx^*}{1+(x^*)^2}, \ \ \tau = \frac{3(x^*)^2-5-bx^*}{1+(x^*)^2} \]となるので、分岐点は
\[ a_c = \frac{5(b+\sqrt{b^2+60})}{6} \]となる。したがって、分岐点近傍でのリミットサイクルの周期は
\[ T = \frac{2 \pi}{\sqrt{\Delta}} = 2 \pi \sqrt{\frac{48+b(b+\sqrt{b^2+60})}{15b(b+\sqrt{b^2+60})}} \approx 4 \pi \sqrt{\frac{ 2 \sqrt{15}}{75b} } \]と見積もることができる。
投稿者:goodbook
投稿日時:2021-05-02 08:24:59
|
|
|
P.318の問題番号「8.4.1」
に対する解答
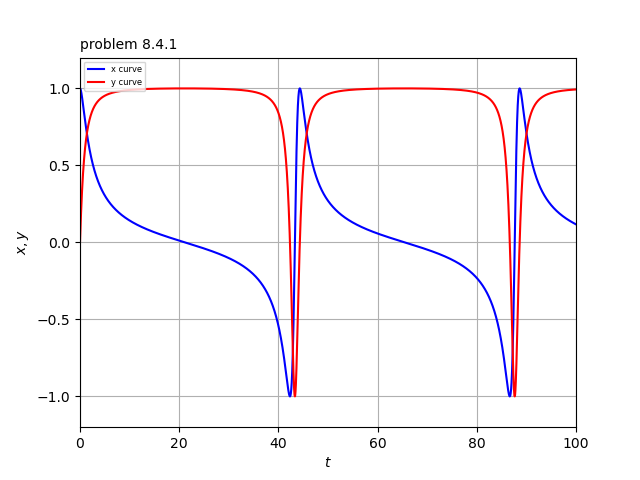
系$\dot{r}=r(1-r^2), \ \ \dot{\theta}=\mu-\sin \theta$
$\mu=1.01$とし、初期値を$r=1, \ \ \theta=0$としたときの$x$および$y$の波形は添付図のようになる。
投稿者:goodbook
投稿日時:2021-05-02 10:11:14
|
|





