|
P.320の問題番号「8.4.12」
に対する解答
点$(\mu,1)$を通過する軌道は安定多様体(ここでは$y$軸)から$\mathcal{O}(\mu)$の距離だけずれた軌道を進み、サドル(ここでは原点)に近づいていく。その後、軌道はサドルから逃げ出し、不安定多様体(ここでは$x$軸)から$\mathcal{O}(\mu)$の距離だけずれた軌道をサドルから離れる方向に進んでいくと考えられる。したがって、軌道がサドルから逃げ出して、$x(t) \approx 1$に達するまでにかかる時間は
\[ T = \int dt \approx \int_{\mu}^1 \frac{dt}{dx} dx = \int_{\mu}^1 \frac{1}{\lambda_u x} dx = \frac{1}{\lambda_u} \ln \left( \frac{1}{\mu} \right) \]と見積もられる。
投稿者:goodbook
投稿日時:2021-05-17 05:43:44
|
|
|
P.320の問題番号「8.5.1」
に対する解答
$f(I)=(\ln I)^{-1}$とおくと、
\[ f^{(1)}=-\frac{1}{(\ln I)^2} \cdot \frac{1}{I} = -\frac{f^2}{I} \ \to \ If^{(1)}=-f^2 \]となる。この式の両辺を$I$で微分していくと、
\[ f^{(n+1)}=-I^{-1} \left( nf^{(n)}+\sum_{i=0}^n a_{i,n-i} f^{(i)} f^{(n-i)} \right) \]という関係式が得られる。ここで、係数$a_{i,n-i}$は
\[ (1+x)^n = \sum_{i=0}^n a_{i,n-i} x^i \]を満たし、また$f^{(0)}=f$とした。
$\ln(I-I_c)$は$I_c$において発散するので、$f(I-I_c)$は$I_c$において$0$となる。次に、$(I-Ic)[ \ln (I-I_c)]^2$は$I_c$において$0$となるので、$f^{(1)}(I-I_c)$は$I_c$において発散する。したがって、上記で求めた$f^{(n+1)}$の関係式を用いると、$f^{(n+1)}(I-I_c)$は$I_c$において発散することがわかる。
投稿者:goodbook
投稿日時:2021-05-19 05:26:45
|
|
|
P.320の問題番号「8.5.2」
に対する解答
駆動された振動子$\phi''+\alpha \phi'+\sin \phi = I$
$y=\phi'$とすると、系は
\[ \phi'=y, \ \ y'=I-\sin \phi - \alpha y \]と表すことができる。
相図1)$\alpha$が一定で十分に小さければ、$I$を減少させることにより、系の安定なリミットサイクル(i)はサドルノード分岐を起こし(ii,iii)、双安定な状態(iii)になる。さらに$I$を減少させると、ホモクリニック分岐を起こし、リミットサイクルは破壊される(iv,v)。
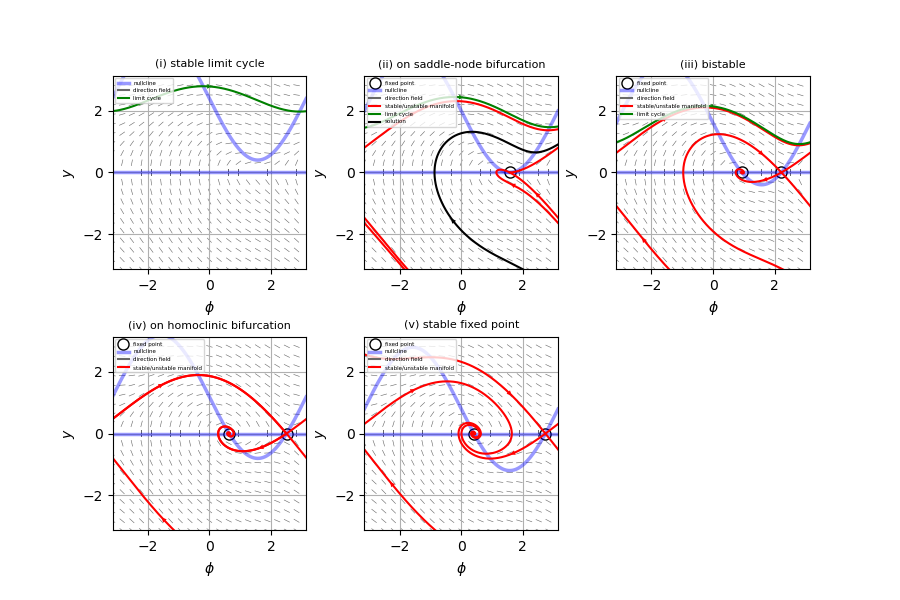
投稿者:goodbook
投稿日時:2021-05-22 08:43:23
|
|
|
P.320の問題番号「8.5.3」
に対する解答
ロジスティック方程式$\dot{N}=rN(1-N/K(t))$ ($K(t)$は正で、tについて滑らかで$T$周期的)
(a) 曲線$N(t)=K(t)$を考える。このとき、$N(t)$の変化はこの曲線より上側では$\dot{N}<0$となり下向き、この曲線より下側では$\dot{N}>0$となり上向きとなる。特に、任意の$N>0$から始まる$N(t)$の値はやがて$K_{\mathrm{min}} \leq N \leq K_{\mathrm{max}} $の細い帯に入り、そこに永久に留まる。
時刻$t=0$で$N$であったものが、$T$時間後に$P(N)$となるポアンカレ写像を考える。$t=0, \ \ N=K_{\mathrm{min}}$で始まる$N$の時間変化を考えると、$P(K_{\mathrm{min}})>K_{\mathrm{min}}$となる。一方、$t=0, \ \ N=K_{\mathrm{max}}$で始まる$N$の時間変化を考えると、$P(K_{\mathrm{max}})<K_{\mathrm{max}}$となる。ポアンカレ写像$P(N)$が単調な連続関数であることを考慮すると、中間値の定理より$P(N)$のグラフは45°の対角線をどこかで横切らなくてはならない。この交点を$N^*$とすると、$P(N^*)=N^*$となり、これは周期$T$のリミットサイクルが存在することを示す。
(b) ポアンカレ写像$P(N)$がある区間で$P(N) \equiv N$となり、無限に多数の閉軌道の帯ができるとする。これらの閉軌道のうち、2つの閉軌道$N_1(t) > N_2(t)$を選らんでくる。この場合、ある時刻$t$において、$N_1(t) > K(t) > N_2(t)$となり、$\dot{N}_1<0. \ \ \dot{N}_2>0$となるはずである。このような$N_1, \ \ N_2$として互いに近接したもので、非常に短い時間間隔$\Delta t$後に、$N_1(t+\Delta t)=N_2(t+\Delta t)=K(t+\Delta t)$となるようなものを選ぶことができるはずである。しかしこれは軌道が互いに交わらないということに反する。したがって、リミットサイクルは唯一であると考えられる。
投稿者:goodbook
投稿日時:2021-05-23 08:48:32
|
|
|
P.320の問題番号「8.6.1」
に対する解答
系$\dot{\theta}_1 = \omega_1+\sin \theta_1 \cos \theta_2, \ \ \dot{\theta}_2 = \omega_2+\sin \theta_2 \cos \theta_1, \ \ \omega_1, \ \omega_2 \geq 0$
(a)(b) まず位相差$\phi=\theta_1-\theta_2$について調べる。このとき、
\[ \dot{\phi}=\dot{\theta}_1-\dot{\theta}_2=\omega_1-\omega_2+\sin \phi \]となる。したがって、
i) $|\omega_1-\omega_2|>1$ならば固定点はなし。
ii) $|\omega_1-\omega_2|=1$ならば1つの固定点、すなわち、半安定な周期解をもつ。
iii) $|\omega_1-\omega_2|<1$ならば2つの固定点、すなわち、安定な位相ロック解と不安定な位相ロック解をもつ。
従って、系は$|\omega_1-\omega_2|=1$で周期軌道のサドルノード分岐を起こすことがわかる。
一方、方程式は
\[ \dot{\theta}_1= \omega_1+\frac{1}{2} \{ \sin (\theta_1+\theta_2)+\sin (\theta_1-\theta_2) \}, \\
\dot{\theta}_2= \omega_2+\frac{1}{2} \{ \sin (\theta_1+\theta_2)-\sin (\theta_1-\theta_2) \} \]と書ける。したがって、
\[ \sin ( \theta_1^*+\theta_2^* ) = -\omega_1-\omega_2, \ \ \sin ( \theta_1^*-\theta_2^* ) = -\omega_1+\omega_2 \]を満たす$(\theta_1^*, \theta_2^*)$を考えると、
i) $\omega_1+\omega_2>1$ならば固定点はなし。
ii) $\omega_1+\omega_2=1$ならば4つの固定点をもち、それぞれ半安定な固定点となる。
iii) $\omega_1+\omega_2<1$ならば$|\omega_1+\omega_2|=1$のときの4つの固定点がそれぞれサドルとノードに別れる。
これは、$\omega_1+\omega_2=1$で無限周期分岐を起こすことを示している。
以上の相図を添付(i)-(v)に示す。
(c) $(\omega_1, \omega_2)$平面上の安定性ダイアグラムを描くと添付図右下のようになる。
$|\omega_1-\omega_2|=1$を満たす直線上に周期軌道のサドルノード分岐をもち、$\omega_1+\omega_2=1$の直線上に無限周期分岐をもつ。
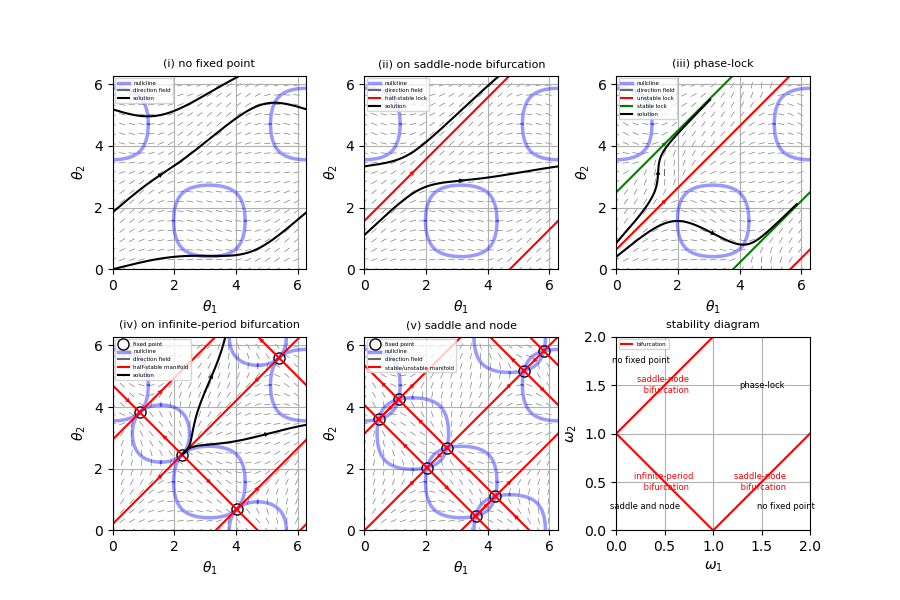
投稿者:goodbook
投稿日時:2021-05-30 13:07:44
|
|
|
P.320の問題番号「8.6.2」
に対する解答
結合振動子系$\dot{\theta}_1 = \omega_1+K_1 \sin (\theta_2-\theta_1), \ \ \dot{\theta}_2 = \omega_2+K_2 \sin (\theta_1-\theta_2)$
(a) この系のヌルクラインは
\[ \sin (\theta_1-\theta_2)=\frac{\omega_1}{K_1}, \ \ \sin (\theta_1-\theta_2)=-\frac{\omega_2}{K_2} \]となるので、$\omega_1,\omega_2>0$および$K_1,K_2>0$ならば系は固定点をもたない。
(b) $\phi=\theta_1-\theta_2, \ \ \varphi=\theta_1+\theta_2$とおくと、
\[ \dot{\phi}=\omega_1-\omega_2-(K_1+K_2)\sin \phi, \ \ \dot{\varphi}=\omega_1+\omega_2-(K_1-K_2)\sin \phi \]の方程式が成り立つ。このとき、
\[ \frac{d \varphi}{d \phi}=\frac{\dot{\varphi}}{\dot{\phi}}=\frac{2\omega^*}{\omega_1-\omega_2-(K_1+K_2)\sin \phi}+\frac{K_1-K_2}{K_1+K_2} \]となる。ここで、
\[ \omega^*=\frac{K_1\omega_2+K_2\omega_1}{K_1+K_2} \]とおいた。この式より
\[ (K_1+K_2)d \varphi=\left[ (K_1-K_2)+\frac{2\omega^*}{s-\sin \phi} \right] d \phi \]と変形して両辺を積分した後、少し整理すると保存量を得ることができる。ここで、\[ s=\frac{\omega_1-\omega_2}{K_1+K_2} \]とおいた。
i) $|\omega_1-\omega_2|<K_1+K_2$のとき、
\[ E=\frac{s \tan(\phi/2)-1+\sqrt{1-s^2} \tanh [(K_1\theta_2+K_2\theta_1) \sqrt{1-s^2}/2\omega^*]}{\sqrt{1-s^2}+(s \tan(\phi/2)-1) \tanh [(K_1\theta_2+K_2\theta_1) \sqrt{1-s^2}/2\omega^*] } \] ii) $|\omega_1-\omega_2|>K_1+K_2$のとき、
\[ E=\frac{s \tan(\phi/2)-1-\sqrt{s^2-1} \tan [(K_1\theta_2+K_2\theta_1) \sqrt{s^2-1}/2\omega^*]}{\sqrt{s^2-1}+(s \tan(\phi/2)-1) \tan [(K_1\theta_2+K_2\theta_1) \sqrt{s^2-1}/2\omega^*] } \]となる。
投稿者:goodbook
投稿日時:2021-06-03 06:04:42
|
|
|
P.321の問題番号「8.6.3」
に対する解答
系$\dot{\theta}_1=\omega_1, \ \ \dot{\theta}_2=\omega_2$、$\omega_1/\omega_2$は無理数。
解)トーラス上の任意の点$(p_1,p_2)$、任意の初期条件$(q_1,q_2)$に対して、$p_1=0, \ \ p_2=q_2$としても一般性は変わらないので、このように設定する。
$\theta_2$方向に軌道が1周するときの時間は$2\pi/\omega_2$であるので、このとき、$\theta_1$方向には$2\pi \omega_1/\omega_2$だけ移動する。したがって、任意の初期条件$(q_1,q_2)$から初めて、$\theta_2$方向に軌道が$n$周したとすると、$\theta_1$方向には
\[ 2\pi \left[ \frac{\omega_1}{\omega_2} n+\delta_0 \right] \]に移動することになる。ここで、記号$[a]$を$a>0$に対してその整数部分を除いたものとして定義し、また、$q_1=2\pi \delta, \ \ 0<\delta_0<1$とおいた。
次に、自然数$n_0$を適切に選ぶと、
\[ \left[ \frac{\omega_1}{\omega_2}n_0+\delta_0 \right] < \min \left( \left[ \frac{\omega_1}{\omega_2} \right], \delta_0 \right) \]とすることができる。このときの$\theta_1$方向の位置を
\[ \delta_1=\left[ \frac{\omega_1}{\omega_2}n_0+\delta_0 \right] \]として、$2\pi \delta_1$とする。さらに、自然数$n_1$を適切に選ぶと、
\[ \left[ \frac{\omega_1}{\omega_2}n_1+\delta_1 \right] < \delta_1 \]とすることができる。このときの$\theta_1$方向の位置を
\[ \delta_2=\left[ \frac{\omega_1}{\omega_2}n_1+\delta_1 \right] \]として、$2\pi \delta_2$とする。
この操作を繰り返していくと、$N$回目の操作で、
\[ 2\pi \delta_N < \varepsilon \]とすることができる。
以上のことから、トーラス上の任意の点$q$から出発した軌道が$p$から距離$\varepsilon$以内を通るような
\[ t=\frac{2\pi}{\omega_2} \sum_{i=0}^N n_i < \infty \]が存在することがわかる。
投稿者:goodbook
投稿日時:2021-06-04 04:22:34
|
|
|
P.321の問題番号「8.6.4」
に対する解答
系$\dot{\theta}_1=E-\sin \theta_1+K \sin(\theta_2-\theta_1), \ \ \dot{\theta}_2=E+\sin \theta_2+K \sin(\theta_1-\theta_2), \ \ E,K \geq 0$
(a) この系のヌルクラインは
\[ E-\sin \theta_1+K \sin(\theta_2-\theta_1)=0, \ \ E+\sin \theta_2+K \sin(\theta_1-\theta_2)=0 \]である。これらの式は以下のように変形できる。
\[ \begin{align}
& E-\cos \frac{\theta_1+\theta_2}{2} \sin \frac{\theta_1-\theta_2}{2}=0 \tag{1} \\
& \left( \sin \frac{\theta_1+\theta_2}{2} + 2K \sin \frac{\theta_1-\theta_2}{2} \right) \cos \frac{\theta_1-\theta_2}{2}=0 \tag{2}
\end{align} \]が得られる。$(2)$式は以下のように分解しておく。
\[ \begin{align}
& \sin \frac{\theta_1+\theta_2}{2} + 2K \sin \frac{\theta_1-\theta_2}{2}=0 \tag{2-1} \\
& \cos \frac{\theta_1-\theta_2}{2}=0 \tag{2-2}
\end{align} \]これらの式を使って固定点を分類する。
i)$E>1$のとき、固定点は存在しない。
ii)$E<1$のとき、$(1)$式と$(2$-$2)$式から2つの固定点
\[(\sin^{-1}E, \pi+\sin^{-1}E), \ \ (\pi-\sin^{-1}E,2\pi-\sin^{-1}E) \]が存在する。
iii)$E<1/\sqrt{2}, \ \ 4KE<1$および$1/\sqrt{2}<E<1, \ \ E^2+4K^2<1$のとき、$(1)$式と$(2$-$1)$式から
\[ \alpha=\sin^{-1}(4KE), \ \ \beta_-=\sin^{-1}\left[\frac{1}{2K} \sqrt{ \frac{1-\sqrt{1-16K^2E^2}}{2} } \right] \]とおいて、2つの固定点
\[ \left(-\frac{\alpha}{2}+\beta_-,2\pi-\frac{\alpha}{2}-\beta_- \right), \left(\pi-\frac{\alpha}{2}-\beta_-,\pi-\frac{\alpha}{2}+\beta_- \right) \]が存在する。
iv)$E<1/\sqrt{2}, \ \ 4KE<1, \ \ E^2+4K^2>1$のとき、$(1)$式と$(2$-$1)$式から
\[ \beta_+=\sin^{-1}\left[\frac{1}{2K} \sqrt{ \frac{1+\sqrt{1-16K^2E^2}}{2} } \right] \]とおいて、2つの固定点
\[ \left(-\frac{\pi}{2}+\frac{\alpha}{2}+\beta_+,\frac{3}{2}\pi+\frac{\alpha}{2}-\beta_+ \right), \left(\frac{\pi}{2}+\frac{\alpha}{2}-\beta_+,\frac{\pi}{2}+\frac{\alpha}{2}+\beta_+ \right) \]が存在する。
以上のことから、
①$E>1$の領域では、固定点なし。
②$E<1/\sqrt{2}, \ \ 4KE<1$および$1/\sqrt{2}<E<1, \ \ E^2+4K^2<1$の領域では、2つの固定点(1つのサドルと1つの不安定ノード)をもつ。
③$E^2+4K^2<1$の領域では、4つの固定点(2つのサドル、1つの安定ノード、1つの不安定ノード)をもつ。
④$E<1/\sqrt{2}, \ \ 4KE<1, \ \ E^2+4K^2>1$の領域では、6つの固定点(3つのサドル、2つの安定ノード、1つの不安定ノード)をもつ。
投稿者:goodbook
投稿日時:2021-06-16 06:21:12
|
|
|
P.321の問題番号「8.6.5」
に対する解答
リサージュ図形$x(t)=\sin t, \ \ y(t)=\sin \omega t$
媒介変数$t$は$0$から$10\pi$まで動かした。
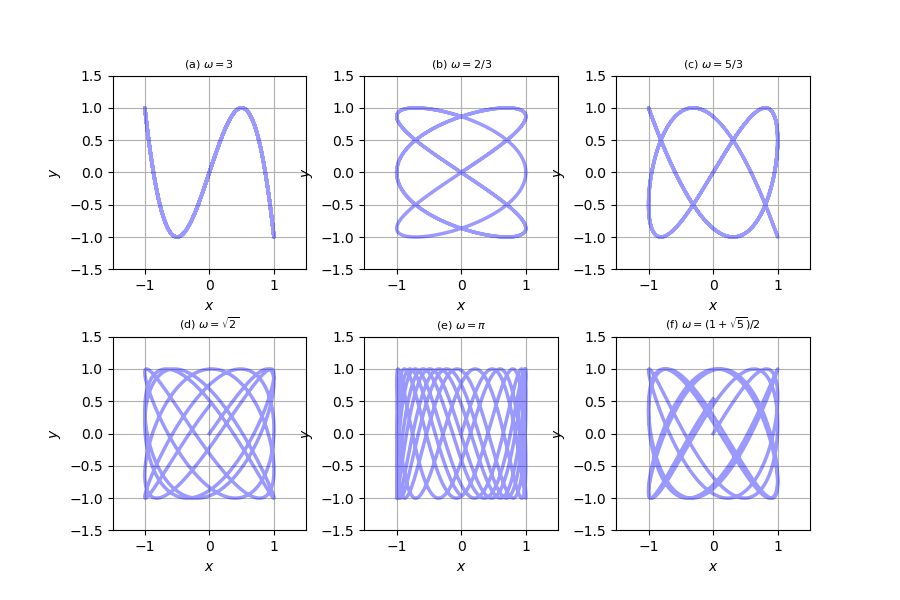
投稿者:goodbook
投稿日時:2021-06-17 06:49:20
|
|
|
P.322の問題番号「8.6.6」
に対する解答
4次元の系$\ddot{x}+x=0, \ \ \ddot{y}+\omega^2 y=0$
(a) この系の一般解は
\[ x(t)=A \sin(t+\alpha), \ \ y(t)=B \sin(\omega t+\beta) \]と書くことができる。ここで、$A,B,\alpha,\beta$は定数である。したがって、もし
\[ x(t)=A(t) \sin \theta(t), \ \ y(t)=B(t) \sin \phi(t) \]と書くならば、
\[ A(t)=A, \ \ B(t)=B, \ \ \theta(t)=t+\alpha, \ \ \phi(t)=\omega t+\beta \]となるので、$\dot{A}=\dot{B}=0$であり、$\dot{\theta}=1, \ \ \dot{\phi}=\omega$となることがわかる。
(b) (a)の結果から、この系の軌道は
\[ x(t)=A \sin(t+\alpha), \ \ \dot{x}(t)=A \cos(t+\alpha), \ \ y(t)=B \sin(\omega t+\beta), \ \ \dot{y}(t)=\omega B \cos(\omega t+\beta) \]と表すことができる。これらの式から、$x(t),\dot{x}(t)$は$(x,\dot{x})$平面中の円上に拘束されており、$y(t),\dot{y}(t)$は$(y,\dot{y})$平面中の楕円上に拘束されていることがわかるので、この系の軌道は4次元の相空間中の2次元のトーラスに拘束されていることがわかる。
(c) リサージュ図形はこの系の軌道を$(x,y)$平面に射影したものと考えられる。
投稿者:goodbook
投稿日時:2021-06-19 08:36:35
|
|





