|
P.322の問題番号「8.6.7」
に対する解答
方程式
\[ m \ddot{r}=\frac{h^2}{mr^3}-k, \ \ \dot{\theta}=\frac{h}{mr^2} \](a) 動径方向の方程式は$\dot{r}=v$とおくと、
\[ \dot{r}=v, \ \ \dot{v}=\frac{h^2}{m^2r^3}-\frac{k}{m} \]と書くことができる。この系の固定点は
\[ \left(\sqrt[3]{\frac{h^2}{mk}},\ 0 \right) \]となり、ヤコビ行列を調べると、この固定点はセンターとなる。したがって、
\[ r_0=\sqrt[3]{\frac{h^2}{mk}}, \ \ \omega_{\theta}=\frac{h}{m r_0^2} \]の一様な円運動に対応する解をもつ。
(b) 円軌道の周りの小さな動径方向の振動の振幅を$r_p$とし、$r=r_0+r_p$とおいて方程式を整理すると、
\[ m \ddot{r}_p=-3\frac{k}{r_0}r_p \]となる。したがって、円軌道の周りの小さな動径方向の振動の振動数$\omega_r$は
\[ \omega_r=\sqrt{\frac{3k}{mr_0}}=\sqrt{3}\omega_{\theta} \]となる。
(c) (b)の結果より$\omega_r/\omega_{\theta}=\sqrt{3}$となるので、この小さな動径方向の振動が準周期運動に対応することがわかる。
(d) 動径方向の方程式は唯一の固定点$(r_0,0)$を持ち、それがセンターであるので、$(r,v)$平面上での軌道は$(r_0,0)$周りの閉軌道となる。つまり、もとの系で軌道を考えると、半径$r_0$の円軌道を基準として、適当な振幅で動径方向に振動するような軌道になる。したがって、この運動は動径方向の振動の任意の振幅に対して、周期的か準周期的になる。
(e) 略解を参照。
投稿者:goodbook
投稿日時:2021-06-27 07:21:55
|
|
|
P.322の問題番号「8.6.8」
に対する解答
方程式
\[ m \ddot{r}=\frac{h^2}{mr^3}-k, \ \ \dot{\theta}=\frac{h}{mr^2} \]
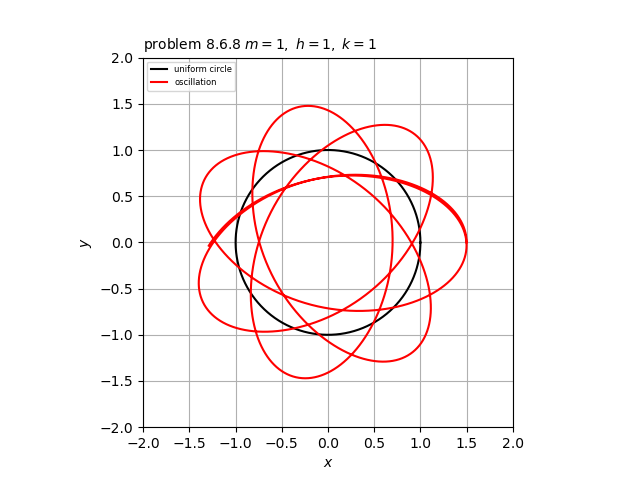
この方程式をコンピュータで解くと、添付図のようになる。
各パラメータは$m=1, \ \ h=1, \ \ k=1$とおいた。このとき、$r_0=1, \ \ \omega_{\theta}=1$となる。
図の黒い円は半径$r_0$の一様な円を表す。また、図の赤い軌道は初期値として$r=1.5, \ \ \theta=0$としたときのものを表す。
投稿者:goodbook
投稿日時:2021-06-29 05:55:09
|
|
|
P.322の問題番号「8.7.1」
に対する解答
\[ \frac{1}{r(1-r^2)}=\frac{1}{r}-\frac{1}{2(r-1)}-\frac{1}{2(r+1)} \]と部分分数を分解すると、
\[ \begin{align} \int_{r_0}^{r_1} \frac{dr}{r(1-r^2)} &= \left[ \ln |r|-\frac{1}{2} \ln |r-1|-\frac{1}{2} \ln |r+1| \right]_{r_0}^{r_1} \\
&= \left[ \ln \frac{r}{\sqrt{r^2-1}} \right]_{r_0}^{r_1} \\
&= \ln \frac{r_1}{\sqrt{r_1^2-1}} - \ln \frac{r_0}{\sqrt{r_0^2-1}} = 2 \pi
\end{align} \]となる。この式を整理すると、
\[ r_1=\left[ 1+e^{-4\pi}(r_0^{-2}-1) \right]^{-\frac{1}{2}} \]が得られる。
また、ポアンカレ写像は
\[ P(r)=\left[ 1+e^{-4\pi}(r^{-2}-1) \right]^{-\frac{1}{2}} \]となるので、
\[ P'(r)=e^{-4\pi}r^{-3}\left[ 1+e^{-4\pi}(r^{-2}-1) \right]^{-\frac{3}{2}} \]から、
\[ P'(r^*)=P'(1)=e^{-4\pi} \]が得られる。
投稿者:goodbook
投稿日時:2021-07-04 08:10:21
|
|
|
P.322の問題番号「8.7.2」
に対する解答
系$\dot{\theta}=1, \ \ \dot{y}=ay$で与えられる円筒上のベクトル場
$S$を円筒上の$\theta=0$の軸とし、$y_0$を$S$上の初期点とする。$\dot{\theta}=1$なので、最初に$S$に戻るのは帰還時間$t=2\pi$の後である。よって、$y_1=P(y_0)$で、$y_1$は
\[ \int_{y_0}^{y_1} \frac{dy}{ay} = \int_0^{2\pi}dt=2\pi \]を満たす。積分を評価すると、
\[ y_1=e^{2\pi a}y_0 \]となる。ゆえに、
\[ P(y)=e^{2\pi a}y \]である。
i) $a>0$のとき、固定点は$y^*=0$となり、1つの周期解をもつ。蜘蛛の巣図法により、この固定点は不安定である。
ii) $a=0$のとき、ポアンカレ写像は45°の直線と一致する。つまり、すべての$y$に対して周期解をもつ。
iii) $a<0$のとき、固定点は$y^*=0$となり、1つの周期解をもつ。蜘蛛の巣図法により、この固定点は安定である。
投稿者:goodbook
投稿日時:2021-07-04 08:53:13
|
|
|
P.322の問題番号「8.7.3」
に対する解答
系
\[ \dot{x}+x=F(t), \ \
F(t) = \begin{cases}
+A & (0<t<T/2) \\
-A & (T/2<t<T)
\end{cases}
\](a) 斉次方程式$\dot{x}+x=0$より、
\[ x(t)=Be^{-t} \]が得られるので、この解の係数を$B(t)$として、$\dot{x}+x=F(t)$に代入すると、
\[ \dot{B}=F(t)e^t \]となる。この式を時刻$0$から$T$まで積分すると、
\[ B(T)-B(0)=-A(e^{\frac{T}{2}}-1)^2 \]となる。したがって、$B(0)=x_0$となることを考慮すると、
\[ x(T) = x_0 e^{-T}-A(1-e^{-\frac{T}{2}})^2 \]が得られる。
(b) $x(T)=x_0$となるとき、周期解をもつので、
\[ x_0 = x_0 e^{-T}-A(1-e^{-\frac{T}{2}})^2 \]より、
\[ x_0 = -A \tanh \frac{T}{4} \]が得られる。これは、唯一の周期解となる。
(c) $T \to 0$のとき、$x(T) \to x_0$となる。これは矩形波の周期が極端に短くなるため、$x$への影響がなくなってしまい、初期位置から動くことがなくなったと考えられる。一方、$T \to \infty$のとき、$x(T) \to -A$となる。これは$t \sim T$では矩形波の値は$-A$となるので、$x$はこの値の影響を受けると考えられる。
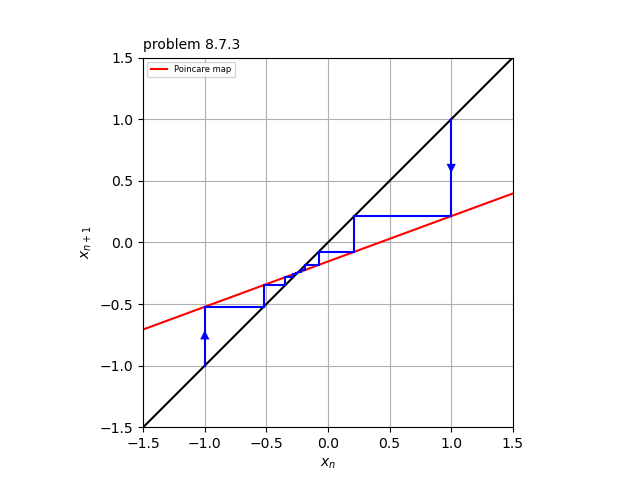
(d) 添付図参照。ただし、$A=1, \ \ T=1$とした。ポアンカレ写像は赤い線。
(e) 添付図参照。クモの巣図法(青い線)を用いると、$P$が大域的に安定な固定点を持つことがわかる。
投稿者:goodbook
投稿日時:2021-07-09 05:43:46
|
|
|
P.323の問題番号「8.7.4」
に対する解答
系$\dot{x}+x=A \sin \omega t , \ \ \omega>0$
この系を初期条件$x(0)=x_0$として解くと、
\[ x(t)=\left(x_0+\frac{\omega A}{1+\omega^2} \right) e^{-t} + \frac{A}{1+\omega^2} \sin \omega t - \frac{\omega A}{1+\omega^2} \cos \omega t \]と得られる。したがって、ポアンカレ写像$P(x_0)$は
\[ P(x_0)=x \left( \frac{2 \pi}{\omega}\right) = x_0 e^{-\frac{2 \pi}{\omega}}-\frac{\omega A}{1+\omega^2} \left(1-e^{-\frac{2 \pi}{\omega}} \right) \]となる。このポアンカレ写像の傾きは$e^{-\frac{2 \pi}{\omega}} < 1$であるので、クモの巣図法により、固定点はただ1つで大域的に安定である。このとき、ポアンカレ写像の切片は$A>0$のとき負の値、$A<0$のとき正の値をとることを考慮すると、固定点$x^*$は$A>0$のとき$x^*<0$、$A<0$のとき$x^*>0$となる。これは固定点の符号を見ることで、$A$の符号を推論できることを示す。
投稿者:goodbook
投稿日時:2021-07-22 05:46:01
|
|
|
P.323の問題番号「8.7.5」
に対する解答
系$\dot{\theta} + \sin \theta = \sin t$
この系は2つの周期解というより、2つの振動解をもつのではないか。
投稿者:goodbook
投稿日時:2021-07-24 07:08:04
|
|
|
P.323の問題番号「8.7.6」
に対する解答
まず、系$\dot{\theta} + \sin \theta = 0$を考えると、$\theta=2n\pi, \ \ (2n+1)\pi$に固定点をもち、それぞれ$\theta=2n\pi$が安定な固定点、$\theta=(2n+1)\pi$が不安定な固定点となる。
これを考慮して、系$\dot{\theta} + \sin \theta = \sin t$を考える。
最初、不安定な固定点付近にある$\theta$は$\sin t$の項がなければ、すぐに安定な固定点に向かうが、$\sin t$の効果により、不安定な固定点の周りでしばらく振動する。この後、適当な時刻で、$\theta$は安定な固定点の方に動き、$\sin t$の効果により、安定な固定点の周りで振動を続ける。
投稿者:goodbook
投稿日時:2021-07-24 07:09:57
|
|
|
P.323の問題番号「8.7.7」
に対する解答
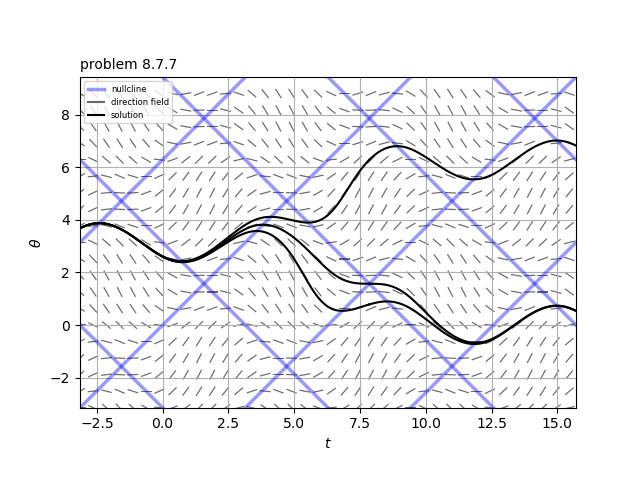
系$\dot{t}=1, \ \ \dot{\theta}=\sin t-\sin \theta$
相図は添付図のようになる。
投稿者:goodbook
投稿日時:2021-07-24 07:11:40
|
|
|
P.323の問題番号「8.7.8」
に対する解答
系$\dot{x}+x=F(t), \ \ F(t)$は滑らかな$T$周期関数
$t=0$のとき$x(0)=x_0$とすると、一般解は
\[ x(t)=\left[x_0+\int_0^tF(t')e^{t'}dt' \right] e^{-t} \]となる。この一般解よりポアンカレ写像$P$は
\[ P(x_0)=x(T)=\left[x_0+\int_0^T F(t)e^tdt \right] e^{-T} \]となる。この$P$のグラフは傾きが$e^{-T}<1$の直線となるので、これは対角線とただ1つの点で交わる。したがって、クモの巣図法により、固定点はただ1つで、大域的に安定である。つまり、系は安定な$T$周期解$x(t)$を必然的にもつと考えられる。
投稿者:goodbook
投稿日時:2021-07-24 10:49:32
|
|





